1.Calculate the heating value of methanol CH3OH given that 0.87g of the fuel burn in air to raise the temperature of 500g of water from 20oC to 27oC.(C-12.0,H=1.0 O=16.0).
Moles of methanol used = Mass of methanol used => 0.87 g = 0.02718 moles
Molar mass of methanol 32
Heat produced ∆H = mass of water(m) x specific heat capacity (c)x ∆T
=> 500 x 4.2 x 7 = 14700 Joules = 14.7 kJ
1000
Molar heat of combustion ∆Hc = Heat produced ∆H
Number of moles of fuel
=> 14.7 kJ = 540.8389 kJmole-1
0.02718 moles
Heating value = molar heat of combustion => 540.8389 kJmole-1 = 16.9012 kJg-1
Molar mass of fuel 32 g
2. 1.0 g of carbon burn in excess air to raise the temperature of 400g of water by 18oC.Determine the molar heat of combustion and hence the heating value of carbon(C-12.0,).
Moles of carbon used = Mass of carbon used => 1.0 g = 0.0833 moles
Molar mass of carbon 12
Heat produced ∆H = mass of water(m) x specific heat capacity (c)x ∆T
=> 400 x 4.2 x 18 = 30240 Joules = 30.24 kJ
1000
Molar heat of combustion ∆Hc = Heat produced ∆H
Number of moles of fuel
=> 30.24 kJ = 363.0252 kJmole-1
0.0833 moles
Heating value = molar heat of combustion => 363.0252 kJmole-1= 30.2521 kJg-1
Molar mass of fuel 12 g
(c)Standard enthalpy/heat of displacement ∆Hᶿd
The molar standard enthalpy/heat of displacement ∆Hᶿd is defined as the energy/heat change when one mole of a substance is displaced from its solution.
A displacement reaction takes place when a more reactive element/with less electrode potential Eᶿ /negative Eᶿ /higher in the reactivity/electrochemical series remove/displace another with less reactive element/with higher electrode potential Eᶿ /positive Eᶿ /lower in the reactivity/electrochemical series from its solution.e.g.
(i)Zn(s) + CuSO4(aq) -> Cu(s) + ZnSO4(aq)
Ionically: Zn(s) + Cu2+(aq) -> Cu(s) + Zn2+ (aq)
(ii)Fe(s) + CuSO4(aq) -> Cu(s) + FeSO4(aq)
Ionically: Fe(s) + Cu2+(aq) -> Cu(s) + Fe2+ (aq)
(iii)Pb(s) + CuSO4(aq) -> Cu(s) + PbSO4(s)
This reaction stops after some time as insoluble PbSO4(s) coat/cover unreacted lead.
(iv)Cl2(g) + 2NaBr(aq) -> Br2(aq) + 2NaCl(aq)
Ionically: Cl2(g)+ 2Br– (aq) -> Br2(aq) + 2Cl– (aq)
Practically, a displacement reaction takes place when a known amount /volume of a solution is added excess of a more reactive metal.
To determine the molar standard enthalpy/heat of displacement(∆Hᶿd) of copper
Procedure
Place 20cm3 of 0.2M copper(II)sulphate(VI)solution into a 50cm3 plastic beaker/calorimeter. Determine and record the temperature of the solution T1.Put all the Zinc powder provided into the plastic beaker. Stir the mixture using the thermometer. Determine and record the highest temperature change to the nearest 0.5oC- T2 . Repeat the experiment to complete table 1 below
Table 1
| Experiment | I | II |
| Final temperature of solution(T2) | 30.0oC | 31.0oC |
| Final temperature of solution(T1) | 25.0oC | 24.0oC |
| Change in temperature(∆T) | 5.0 | 6.0 |
Questions
1.(a) Calculate:
(i)average ∆T
Average∆T = change in temperature in experiment I and II
=>5.0 + 6.0 = 5.5oC
2
(ii)the number of moles of solution used
Moles used = molarity x volume of solution = 0.2 x 20 = 0.004 moles
1000 1000
(iii)the enthalpy change ∆H for the reaction
Heat produced ∆H = mass of solution(m) x specific heat capacity (c)x ∆T
=> 20 x 4.2 x 5.5 = 462 Joules = 0.462 kJ
1000
(iv)State two assumptions made in the above calculations.
Density of solution = density of water = 1gcm-3
Specific heat capacity of solution=Specific heat capacity of solution=4.2 kJ-1kg-1K
This is because the solution is assumed to be infinite dilute.
2. Calculate the enthalpy change for one mole of displacement of Cu2+ (aq) ions.
Molar heat of displacement ∆Hd = Heat produced ∆H
Number of moles of fuel
=> 0.462 kJ = 115.5 kJmole-1
0.004
3.Write an ionic equation for the reaction taking place.
Zn(s) + Cu2+(aq) -> Cu(s) + Zn2+(aq)
4.State the observation made during the reaction.
Blue colour of copper(II)sulphate(VI) fades/becomes less blue/colourless.
Brown solid deposits are formed at the bottom of reaction vessel/ beaker.
5.Illustrate the above reaction using an energy level diagram.
Zn(s) + Cu2+(aq)
Energy ∆H = -115.5 kJmole-1
(kJ)
Cu(s) + Zn2+(aq)
Reaction progress/path/coordinates
6. Iron is less reactive than Zinc. Explain the effect of using iron instead of Zinc on the standard molar heat of displacement ∆Hd of copper(II)sulphate (VI) solution.
No effect.Cu2+ (aq) are displaced from their solution.The element used to displace it does not matter.The reaction however faster if a more reactive metal is used.
7.(a)If the standard molar heat of displacement ∆Hd of copper(II)sulphate (VI) solution is 209kJmole-1 calculate the temperature change if 50cm3 of 0.2M solution was displaced by excess magnesium.
Moles used = molarity x volume of solution = 0.2 x 50 = 0.01 moles
1000 1000
Heat produced ∆H = Molar heat of displacement ∆Hd x Number of moles
=>209kJmole-1x 0.01 moles = 2.09 kJ
∆T (change in temperature) = Heat produced ∆H Molar heat of displacement ∆Hd x Number of moles
=>2.09 kJ = 9.9524Kelvin
0.01 moles
(b)Draw an energy level diagram to show the above energy changes
Mg(s) + Cu2+(aq)
Energy ∆H = -209 kJmole-1
(kJ)
Cu(s) + Mg2+(aq)
Reaction progress/path/coordinates
8. The enthalpy of displacement ∆Hd of copper(II)sulphate (VI) solution is 12k6kJmole-1.Calculate the molarity of the solution given that 40cm3 of this solution produces 2.204kJ of energy during a displacement reaction with excess iron filings.
Number of moles = Heat produced ∆H Molar heat of displacement ∆Hd
=>2.204 kJ = 0.0206moles
126 moles
Molarity of the solution = moles x 1000 Volume of solution used
= 0.0206moles x 1000 = 0.5167 M
40
9. If the molar heat of displacement of Zinc(II)nitrate(V)by magnesium powder is 25.05kJmole-1 ,calculate the volume of solution which must be added 0.5 moles solution if there was a 3.0K rise in temperature.
Heat produced ∆H = Molar heat of displacement ∆Hd x Number of moles
=>25.08kJmole-1x 0.5 moles = 1.254 kJ x 1000 =1254J
Mass of solution (m) = Heat produced ∆H
specific heat capacity (c)x ∆T
=> 1254J = 99.5238 g
4.2 x 3
Volume = mass x density = 99.5238 g x 1 = 99.5238cm3
Note: The solution assumes to be too dilute /infinite dilute such that the density and specific heat capacity is assumed to be that of water.
Graphical determination of the molar enthalpy of displacement of copper
Procedure:
Place 20cm3 of 0.2M copper(II)sulphate (VI) solution into a calorimeter/50cm3 of plastic beaker wrapped in cotton wool/tissue paper.
Record its temperature at time T= 0.
Stir the solution with the thermometer carefully and continue recording the temperature after every 30 seconds .
Place all the (1.5g) Zinc powder provided.
Stir the solution with the thermometer carefully and continue recording the temperature after every 30 seconds for five minutes.
Determine the highest temperature change to the nearest 0.5oC.
Sample results
| Time oC | 0.0 | 30.0 | 60.0 | 90.0 | 120.0 | 150.0 | 180.0 | 210.0 | 240.0 | 270.0 |
| Temperature | 25.0 | 25.0 | 25.0 | 25.0 | 25.0 | xxx | 36.0 | 35.5 | 35.0 | 34.5 |
Sketch graph of temperature against time
36.5
Extrapolation
Temperature point ∆T
oC
130 Time(seconds)
Questions
- Show and determine the change in temperature ∆T
From a well constructed graph ∆T= T2 –T1 at 150 second by extrapolation
∆T = 36.5 – 25.0 = 11.5oC
2.Calculate the number of moles of copper(II) sulphate(VI)used given the molar heat of displacement of Cu2+ (aq)ions is 125kJmole-1
Heat produced ∆H = mass of solution(m) x specific heat capacity (c)x ∆T
=> 20 x 4.2 x 11.5 = 966 Joules = 0.966 kJ
1000
Number of moles = Heat produced ∆H Molar heat of displacement ∆Hd
=>.966 kJ = 0.007728moles
125 moles 7.728 x 10-3moles
- What was the concentration of copper(II)sulphate(VI) in moles per litre.
Molarity = moles x 1000 => 7.728 x 10-3moles x 1000 = 0.3864M
Volume used 20
4.The actual concentration of copper(II)sulphate(VI) solution was 0.4M.Explain the differences between the two.
Practical value is lower than theoretical. Heat/energy loss to the surrounding and that absorbed by the reaction vessel decreases ∆T hence lowering the practical number of moles and molarity against the theoretical value
5.a) In an experiment to determine the molar heat of reaction when magnesium displaces copper ,0.15g of magnesium powder were added to 25.0cm3 of 2.0M copper (II) chloride solution. The temperature of copper (II) chloride solution was 25oC.While that of the mixture was 43oC.
i)Other than increase in temperature, state and explain the observations which were made during the reaction.(3mks)
ii)Calculate the heat change during the reaction (specific heat capacity of the solution = 4.2jg-1k-1and the density of the solution = 1g/cm3(2mks)
iii)Determine the molar heat of displacement of copper by magnesium.(Mg=24.0).
iv)Write the ionic equation for the reaction.(1mk)
v)Sketch an energy level diagram for the reaction.(2mks)
(c)Standard enthalpy/heat of neutralization ∆Hᶿn
The molar standard enthalpy/heat of neutralization ∆Hᶿn is defined as the energy/heat change when one mole of a H+ (H3O+)ions react completely with one mole of OH– ions to form one mole of H2O/water.
Neutralization is thus a reaction of an acid /H+ (H3O+)ions with a base/alkali/ OH– ions to form salt and water only.
Strong acids/bases/alkalis are completely dissociated to many free ions(H+ /H3O+ and OH– ions).
Weak acids/bases/alkalis are partially dissociated to few free ions(H+ (H3O+ and OH– ions) and exist more as molecules.
Neutralization is an exothermic(-∆H) process.The enrgy produced during neutralization depend on the amount of free ions (H+ H3O+ and OH–)ions existing in the acid/base/alkali reactant:
(i)for weak acid-base/alkali neutralization,some of the energy is used to dissociate /ionize the molecule into free H+ H3O+ and OH– ions therefore the overall energy evolved is comparatively lower/lesser/smaller than strong acid / base/ alkali neutralizations.
(ii) (i)for strong acid/base/alkali neutralization, no energy is used to dissociate /ionize since molecule is wholly/fully dissociated/ionized into free H+ H3O+ and OH– ions.The overall energy evolved is comparatively higher/more than weak acid-base/ alkali neutralizations. For strong acid-base/alkali neutralization, the enthalpy of neutralization is constant at about 57.3kJmole-1 irrespective of the acid-base used. This is because ionically:
OH–(aq)+ H+(aq) -> H2O(l) for any wholly dissociated acid/base/alkali
Practically ∆Hᶿn can be determined as in the examples below:
To determine the molar enthalpy of neutralization ∆Hn of Hydrochloric acid
Procedure
Place 50cm3 of 2M hydrochloric acid into a calorimeter/200cm3 plastic beaker wrapped in cotton wool/tissue paper. Record its temperature T1.Using a clean measuring cylinder, measure another 50cm3 of 2M sodium hydroxide. Rinse the bulb of the thermometer in distilled water. Determine the temperature of the sodium hydroxide T2.Average T2 andT1 to get the initial temperature of the mixture T3.
Carefully add all the alkali into the calorimeter/200cm3 plastic beaker wrapped in cotton wool/tissue paper containing the acid. Stir vigorously the mixture with the thermometer.
Determine the highest temperature change to the nearest 0.5oC T4 as the final temperature of the mixture. Repeat the experiment to complete table 1.
Table I . Sample results
| Experiment | I | II |
| Temperature of acid T1 (oC) | 22.5 | 22.5 |
| Temperature of base T2 (oC) | 22.0 | 23.0 |
| Final temperature of solution T4(oC) | 35.5 | 36.0 |
| Initial temperature of solution T3(oC) | 22.25 | 22.75 |
| Temperature change( T5) | 13.25 | 13.75 |
(a)Calculate T6 the average temperature change T6 = 13.25 +13.75 = 13.5 oC 2
(b)Why should the apparatus be very clean?
Impurities present in the apparatus reacts with acid /base lowering the overall temperature change and hence ∆Hᶿn.
(c)Calculate the:
(i)number of moles of the acid used
number of moles = molarity x volume => 2 x 50 = 0.1moles 1000 1000
(ii)enthalpy change ∆H of neutralization.
∆H = (m)mass of solution(acid+base) x (c)specific heat capacity of solution x ∆T(T6) => (50 +50) x 4.2 x 13.5 = 5670Joules = 5.67kJ
(iii) the molar heat of neutralization the acid.
∆Hn = Enthalpy change ∆H => 5.67kJ = 56.7kJ mole-1
Number of moles 0.1moles
(c)Write the ionic equation for the reaction that takes place
OH–(aq)+ H+(aq) -> H2O(l)
(d)The theoretical enthalpy change is 57.4kJ. Explain the difference with the results above.
The theoretical value is higher
Heat/energy loss to the surrounding/environment lowers ∆T/T6 and thus ∆Hn
Heat/energy is absorbed by the reaction vessel/calorimeter/plastic cup lowers ∆T and hence ∆Hn
(e)Compare the ∆Hn of the experiment above with similar experiment repeated with neutralization of a solution of:
(i) potassium hydroxide with nitric(V) acid
The results would be the same/similar.
Both are neutralization reactions of strong acids and bases/alkalis that are fully /wholly dissociated into many free H+ / H3O+ and OH– ions.
(ii) ammonia with ethanoic acid
The results would be lower/∆Hn would be less.
Both are neutralization reactions of weak acids and bases/alkalis that are partially /partly dissociated into few free H+ / H3O+ and OH– ions. Some energy is used to ionize the molecule.
(f)Draw an energy level diagram to illustrate the energy changes
H2 H+(aq)+OH–(aq)
Energy
(kJ)
∆H = -56.7kJ
H1 H2O (l)
Reaction path/coordinate/progress
Theoretical examples
1.The molar enthalpy of neutralization was experimentary shown to be 51.5kJ per mole of 0.5M hydrochloric acid and 0.5M sodium hydroxide. If the volume of sodium hydroxide was 20cm3, what was the volume of hydrochloric acid used if the reaction produced a 5.0oC rise in temperature?
Working:
Moles ofsodium hydroxide = molarity x volume => 0.5 M x 20cm3 = 0.01 moles
1000 1000
Enthalpy change∆H = ∆Hn => 51.5 = 0.515kJ
Molessodium hydroxide 0.01 moles
Mass of base + acid = Enthalpy change∆H in Joules
Specific heat capacity x ∆T
=> 0.515kJ x 1000 = 24.5238g
4.2 x 5
Mass/volume of HCl = Total volume – volume of NaOH
=>24.5238 – 20.0 = 4.5238 cm3
- ∆Hn of potassium hydroxide was practically determined to be 56.7kJmole-1.Calculate the molarity of 50.0 cm3 potassium hydroxide used to neutralize 25.0cm3 of dilute sulphuric(VI) acid raising the temperature of the solution from 10.0oC to 16.5oC.
∆H = (m)mass of solution(acid+base) x (c)specific heat capacity of solution x ∆T
=> (50 +25) x 4.2 x 6.5 = 2047.5Joules
Molespotassium hydroxide =Enthalpy change∆H
∆Hn
2047.5Joules = 0.0361 moles
56700Joules
Molarity of KOH = moles x 1000 => 0.0361 moles x 1000 = 0.722M
Volume used 50cm3
3.Determine the specific heat capacity of a solution of a solution mixture of 50.0cm3 of 2M potassium hydroxide neutralizing 50.0cm3 of 2M nitric(V) acid if a 13.25oC rise in temperature is recorded.(1mole of potassium hydroxide produce 55.4kJ of energy)
Moles ofpotassium hydroxide = molarity KOH x volume
1000
=> 2 M x 50cm3 = 0.1 moles
1000
Enthalpy change∆H = ∆Hn x Molespotassium hydroxide => 55.4kJ x 0.1 moles = 5.54kJ x 1000=5540Joules
Specific heat capacity = Enthalpy change∆H in Joules
Mass of base + acid x ∆T
=> 5540 = 4.1811J-1g-1K-1
(50+50) x 13.25
Graphically ∆Hn can be determined as in the example below:
Procedure
Place 8 test tubes in a test tube rack .Put 5cm3 of 2M sodium hydroxide solution into each test tube.
Measure 25cm3 of 1M hydrochloric acid into 100cm3 plastic beaker.
Record its initial temperature at volume of base =0. Put one portion of the base into the beaker containing the acid.
Stir carefully with the thermometer and record the highest temperature change to the nearest 0.5oC.
Repeat the procedure above with other portions of the base to complete table 1 below
Table 1:Sample results.
| olume of acid(cm3) | 25.0 | 25.0 | 25.0 | 25.0 | 25.0 | 25.0 | 25.0 | 25.0 | 25.0 |
| Volume of alkali(cm3) | 0 | 5.0 | 10.0 | 15.0 | 20.0 | 25.0 | 30.0 | 35.0 | 40.0 |
| Final temperature(oC) | 22.0 | 24.0 | 26.0 | 28.0 | 28.0 | 27.0 | 26.0 | 25.0 | 24.0 |
| Initial temperature(oC) | 22.0 | 22.0 | 22.0 | 22.0 | 22.0 | 22.0 | 22.0 | 22.0 | 22.0 |
| Change in temperature | 0.0 | 2.0 | 4.0 | 6.0 | 6.0 | 5.0 | 4.0 | 3.0 | 2.0 |
(a)Complete the table to determine the change in temperature.
(b)Plot a graph of volume of sodium hydroxide against temperature change.
6.7=T2
| Volume of sodium hydroxide(cm3) |
| 0 =T1 |
∆T (oC)
From the graph show and determine :
(i)the highest temperature change ∆T
∆T =T2-T1 => highest temperature-T2 (from extrapolating a correctly plotted graph) less lowest temperature at volume of base=0 :T1
=>∆T = 6.7 – 0.0 = 6.70C
(ii)the volume of sodium hydroxide used for complete neutralization
From a correctly plotted graph – 16.75cm3
(c)Calculate the number of moles of the alkali used
Moles NaOH = molarity x volume =>2M x 16.75cm3 = 0.0335 moles
1000 1000
(d)Calculate ∆H for the reaction
∆H = mass of solution(acid+base) x c x ∆T
=>(25.0 + 16.75) x 4.2 x 6.7 = 1174.845 J = 1.174845kJ
1000
(e)Calculate the molar enthalpy of neutralization of the alkali.
∆Hn = ∆Hn = 1.174845kJ = 35.0701kJ
Number of moles 0.0335
(d)Standard enthalpy/heat of solution ∆Hᶿs
The standard enthalpy of solution ∆Hᶿsis defined as the energy change when one mole of a substance is dissolve in excess distilled water to form an infinite dilute solution. An infinite dilute solution is one which is too dilute to be diluted further.
Dissolving a solid involves two processes:
(i) breaking the crystal of the solid into free ions(cations and anion).This process is the opposite of the formation of the crystal itself. The energy required to form one mole of a crystal structure from its gaseous ions is called Lattice energy/heat/enthalpy of lattice (∆Hl).Lattice energy /heat/enthalpy of lattice (∆Hl) is an endothermic process (+∆Hl).
The table below shows some ∆Hl in kJ for the process MX(s) -> M+ (g) + X– (g)
| Li | Na | K | Ca | Mg | |
| F | +1022 | +900 | +800 | +760 | +631 |
| Cl | +846 | +771 | +690 | +2237 | +2493 |
| Br | +800 | +733 | +670 | +2173 | +2226 |
(ii)surrounding the free ions by polar water molecules. This process is called hydration. The energy produced when one mole of ions are completely hydrated is called hydration energy/ heat/enthalpy of hydration(∆Hh).Hydration energy /enthalpy of hydration(∆Hh) is an exothermic process(∆Hh).
The table below shows some ∆Hhin kJ for some ions;
| ion | Li+ | Na+ | K+ | Mg2+ | Ca2+ | F– | Cl– | Br– |
| ∆Hh | -1091 | -406 | -322 | -1920 | -1650 | -506 | -364 | -335 |
The sum of the lattice energy +∆Hl(endothermic) and hydration energy -∆Hh (exothermic) gives the heat of solution-∆Hs
∆Hs = ∆Hl +∆Hh
Note
Since ∆Hl is an endothermic process and ∆Hh is an exothermic process then ∆Hs is:
(i)exothermic if ∆Hl is less than ∆Hh and hence a solid dissolve easily in water.
(ii)endothermic if ∆Hl is more than ∆Hh and hence a solid does not dissolve easily in water.
(a)Dissolving sodium chloride crystal/s:
(i) NaCl –—breaking the crystal into free ions–-> Na +(g)+ Cl–(g) ∆Hl =+771 kJ
(ii) Hydrating the ions;
Na +(g) + aq -> Na(aq) ∆Hh = – 406 kJ
Cl–(g) + aq -> Cl–(aq) ∆Hh = – 364 kJ
∆Hs =∆Hh +∆Hs ->(- 406 kJ + – 364 kJ) + +771 kJ = + 1.0 kJmole-1
NaCl does not dissolve easily in water because overall ∆Hs is endothermic
Solubility of NaCl therefore increases with increase in temperature.
Increase in temperature increases the energy to break the crystal lattice of NaCl to freeNa +(g)+ Cl–(g)
(b)Dissolving magnesium chloride crystal/s// MgCl2 (s) ->MgCl2 (aq)
(i) MgCl2 –-breaking the crystal into free ions-->Mg 2+(g)+ 2Cl–(g) ∆Hl =+2493 kJ
(ii) Hydrating the ions;
Mg 2+(g) + aq -> Mg 2+(g) (aq) ∆Hh = – 1920 kJ
2Cl–(g) + aq -> 2Cl–(aq) ∆Hh = (- 364 x 2) kJ
∆Hs =∆Hh +∆Hs -> (- 1920 kJ + (- 364 x 2 kJ)) + +2493 kJ = –155.0 kJmole-1
MgCl2 (s) dissolve easily in water because overall ∆Hs is exothermic .
Solubility of MgCl2 (s) therefore decreases with increase in temperature.
(c)Dissolving Calcium floride crystal/s// CaF2 (s) -> CaF2 (aq)
(i) CaF2 –>Ca 2+(g)+ 2F–(g) ∆Hl =+760 kJ
(ii) Hydrating the ions;
Ca 2+(g) + aq -> Ca 2+(g) (aq) ∆Hh = – 1650 kJ
2F–(g) + aq -> 2F–(aq) ∆Hh = (- 506 x 2) kJ
∆Hs =∆Hh +∆Hs -> (- 1650 kJ + (- 506 x 2 kJ)) + +760 kJ = –1902.0 kJmole-1
CaF2 (s) dissolve easily in water because overall ∆Hs is exothermic .
Solubility of CaF2 (s) therefore decreases with increase in temperature.
(d)Dissolving magnesium bromide crystal/s// MgBr2 (s) ->MgBr2 (aq)
(i) MgCl2 –-breaking the crystal into free ions-->Mg 2+(g)+ 2Br–(g) ∆Hl =+2226 kJ
(ii) Hydrating the ions;
Mg 2+(g) + aq -> Mg 2+(g) (aq) ∆Hh = – 1920 kJ
2Br–(g) + aq -> 2Br–(aq) ∆Hh = (- 335x 2) kJ
∆Hs =∆Hh +∆Hs -> (- 1920 kJ + (- 335 x 2 kJ)) + +2226 kJ = –364.0 kJmole-1
MgBr2 (s) dissolve easily in water because overall ∆Hs is exothermic .
Solubility of MgBr2(s) therefore decreases with increase in temperature.
Practically the heat of solution can be determined from dissolving known amount /mass/volume of solute in known mass /volume of water/solvent.
From the temperature of solvent before and after dissolving the change in temperature(∆T) during dissolution is determined.
To determine the ∆Hs ammonium nitrate
Place 100cm3 of distilled water into a plastic beaker/calorimeter. Determine its temperature and record it at time =0 in table I below.
Put all the 5.0g of ammonium nitrate (potassium nitrate/ammonium chloride can also be used)provided into the plastic beaker/calorimeter, stir using a thermometer and record the highest temperature change to the nearest 0.5oCafter every ½ minute to complete table I.
Continue stirring the mixture throughout the experiment.
Sample results: Table I
| Time (minutes) | 0.0 | ½ | 1 | 1 ½ | 2 | 2 ½ | 3 | 3 ½ |
| Temperature()oC | 22.0 | 21.0 | 20.0 | 19.0 | 19.0 | 19.5 | 20.0 | 20.5 |
(a)Plot a graph of temperature against time(x-axis)
(h) 100cm3 of distilled water at 25oC was added carefully 3cm3 concentrated sulphuric(VI)acid of density 1.84gcm-3.The temperature of the mixture rose from 250C to 38oC.Calculate the molar heat of solution of sulphuric(VI)acid (S=32.0,H=1.0,0=16.0)
Working
Molar mass of H2SO4 = 98g
Mass of H2SO4= Density x volume => 1.84gcm-3 x 3cm3 = 5.52 g
Mass of H2O = Density x volume => 1.00gcm-3 x 100cm3 = 100 g
Moles of H2SO4= mass => 5.52 g = 0.0563 moles
Molar mass of H2SO4 98g
Enthalpy change ∆H= (mass of acid + water) x specific heat capacity of water x ∆T => (100 +5.52 g) x 4.2 x 13oC = 5761.392 J = 5.761392 kJ
1000
∆Hs of H2SO4= ∆H => 5.761392 kJ = -102.33378kJmoles-1
Moles of H2SO4 0.0563 moles
(e)Standard enthalpy/heat of formation ∆Hᶿf
The molar enthalpy of formation ∆Hᶿf is defined as the energy change when one mole of a compound is formed from its elements at 298K(25oC) and 101325Pa(one atmosphere)pressure. ∆Hᶿf is practically difficult to determine in a school laboratory.
It is determined normally determined by applying Hess’ law of constant heat summation.
Hess’ law of constant heat summation states that “the total enthalpy/heat/energy change of a reaction is the same regardless of the route taken from reactants to products at the same temperature and pressure”.
Hess’ law of constant heat summation is as a result of a series of experiments done by the German Scientist Henri Hess(1802-1850). He found that the total energy change from the reactants to products was the same irrespective of the intermediate products between.
Examples of applying Hess’ law of constant heat summation
1.Calculate the molar enthalpy of formation of methane (CH4) given that ∆Hᶿc of carbon-graphite is -393.5kJmole-1,Hydrogen is -285.7 kJmole-1 and that of methane is 890 kJmole-1
Working
Carbon-graphite ,hydrogen and oxygen can react to first form methane.
Methane will then burn in the oxygen present to form carbon(IV)oxide and water. Carbon-graphite can burn in the oxygen to form carbon(IV)oxide.
Hydrogen can burn in the oxygen to form water.
C(s)+ 2H2 (g)+2O2 (g) —∆H1–> CH4(g) +2O2(g) —∆H2–> CO2(g)+2H2O(l)
C(s)+ 2H2 (g)+2O2 (g) —∆H3–> CO2(g)+2H2O(l)
Energy cycle diagram
C(s) + 2H2 (g) + 2O2(g) ∆H1=∆Hᶿc =-890.4kJ CH4(g)+2O2(g)
∆H3=∆Hᶿc =-393.5kJ ∆H3=∆Hᶿc =-285.7kJ x 2 ∆H2= ∆Hᶿf= x
CO2(g) + 2H2O(l)
Substituting:
∆H3 = ∆H1 + ∆H2
-393.5 + (-285.7 x 2) = -890.4kJ + x
x = -74.5 kJ
Heat of formation ∆Hᶿf CH4 = -74.5 kJmole-1
2. Calculate the molar enthalpy of formation of ethyne (C2H2) given : ∆Hᶿc of carbon-graphite = -394kJmole-1,Hydrogen = -286 kJmole-1 , (C2H2) = -1300 kJmole-1
Working
Carbon-graphite ,hydrogen and oxygen can react to first form ethyne.
Ethyne will then burn in the oxygen present to form carbon(IV)oxide and water. Carbon-graphite can burn in the oxygen to form carbon(IV)oxide.
Hydrogen can burn in the oxygen to form water.
2C(s)+ H2 (g)+2 ½ O2 (g) —∆H1–> C2H2 (g) +2 ½ O2(g) —∆H2–> CO2(g)+H2O(l)
2C(s)+ H2 (g)+ 2 ½ O2 (g) —∆H3–> 2CO2(g)+H2O(l)
Energy cycle diagram
2C(s) + H2 (g) +2½O2(g) ∆H1=∆Hᶿf =x C2H2+2½O2(g)
∆H3=∆Hᶿc =-394kJx 2 ∆H3=∆Hᶿc =-286kJ ∆H2= ∆Hᶿc= -1300kJ
2CO2(g) + H2O(l)
Substituting:
∆H3 = ∆H1 + ∆H2
( -394 x 2) + -286 = -1300kJ + x
x = +244 kJ
Heat of formation ∆Hᶿf CH4 = +244 kJmole-1
3. Calculate the molar enthalpy of formation of carbon(II)oxide (CO) given : ∆Hᶿc of carbon-graphite = -393.5kJmole-1, ∆Hᶿc of carbon(II)oxide (CO)= -283 kJmole-1
Working
Carbon-graphite reacts with oxygen first to formcarbon (II)oxide (CO).
Carbon(II)oxide (CO) then burn in the excess oxygen to form carbon(IV)oxide. Carbon-graphite can burn in excess oxygen to form carbon (IV) oxide.
C(s)+ ½O2 (g) —∆H1–> CO (g) + ½ O2(g) —∆H2–> CO2(g)
C(s)+ O2 (g) —∆H3–> CO2(g)
4.Study the information below:
H2(g) + ½ O2(g) -> H2O(l) ∆H1=-286 kJmole-1
C(s) + O2(g) -> CO2(g) ∆H2=-393 kJmole-1
2C(s) + H2(g) + ½ O2(g) ->C2H5OH(l) ∆H3=-277 kJmole-1
Use the information to calculate the molar enthalpy of combustion ∆H4 of ethanol
Energy cycle diagram
2C(s) + 3H2 (g) +3½O2(g) ∆H3=∆Hᶿf =-227kJ C2H5OH +3O2(g)
∆H2=∆Hᶿc =-394kJx 2 ∆H1=∆Hᶿc =-286kJx 3 ∆H4= ∆Hᶿc= x
2CO2(g) + 3H2O(l)
Substituting:
∆H1 + ∆H2 = ∆H3 + ∆H4
( -394 x 2) + -286 x 3 = -277 + x
∆H4 = -1369 kJ
Heat of combustion ∆Hᶿc C2H5OH = -1369 kJmole-1
5.Given the following information below:
CuSO4(s) + (aq) -> CuSO4(aq) ∆H=-66.1 kJmole-1
CuSO4(s) + (aq) + 5H2O(l)-> CuSO4 .5H2O (aq) ∆H=-77.4 kJmole-1
Calculate ∆H for the reaction;
CuSO4(aq) + 5H2O-> CuSO4 .5H2O (aq) ∆H=-77.4 kJmole-1
Working
CuSO4(s) + (aq) + 5H2O(l)-> CuSO4(aq)+ 5H2O(l)-> CuSO4 .5H2O (aq)
CuSO4(s) + (aq) + 5H2O(l)-> CuSO4 .5H2O (aq)
Energy cycle diagram
CuSO4(s) + (aq) + 5H2O(l) ∆H1=+66.1kJ CuSO4(aq)+ 5H2O(l)
∆H3= =-77.4kJ ∆H2= x
CuSO4 .5H2O (aq)
Substituting:
∆H3 = ∆H2 + ∆H1
( -77.4kJ = x + +66.1kJ
∆H4 = -10.9 kJ
Heat of dissolution of CuSO4 = -10.9kJmole-1
Practically, Hess’ law can be applied practically as in the following examples
a)Practical example 1
Determination of the enthalpy of formation of CuSO4.5H2O
Experiment I
Weigh accurately 12.5 g of copper(II)sulphate(VI)pentahydrate. Measure 100cm3 of distilled water into a beaker. Determine its temperature T1 .Put all the crystals of the copper(II)sulphate(VI)pentahydrate carefully into the beaker. Stir using a thermometer and determine the highest temperature change T2 Repeat the procedure again to complete table 1.
Table 1:Sample results
| Experiment | I | II |
| Highest /lowest temperature T2 | 27.0 | 29.0 |
| Initial temperature T1 | 24.0 | 25.0 |
| Change in temperature ∆T | 3.0 | 4.0 |
Experiment II
Weigh accurately 8.0g of anhydrous copper(II)sulphate(VI). Measure 100cm3 of distilled water into a beaker. Determine its temperature T1 .Put all the crystals of the copper(II)sulphate(VI)pentahydrate carefully into the beaker. Stir using a thermometer and determine the highest temperature change T2 Repeat the procedure again to complete table II.
Table II :Sample results
| Experiment | I | II |
| Highest /lowest temperature T2 | 26.0 | 27.0 |
| Initial temperature T1 | 25.0 | 25.0 |
| Change in temperature ∆T | 1.0 | 2.0 |
Questions
(a)Calculate the average ∆T in
(i)Table I
∆T= T2 -T1 => 3.0 +4.0 = 3.5 oC
2
(ii)Table II
∆T= T2 -T1 => 1.0 +2.0 = 1.5 oC
2
(b)Calculate the number of moles of solid used in:
(i)Experiment I
Moles of CuSO4.5H2O = Mass => 12.5 = 0.05 moles
Molar mass 250
(ii)Experiment II
Moles of CuSO4 = Mass => 8.0 = 0.05 moles
Molar mass 160
(c)Calculate the enthalpy change for the reaction in:
(i)Experiment I
Enthalpy change of CuSO4.5H2O= mass of Water(m) x c x ∆T
=>100cm3 x 4.2 x 3.5 oC = -1.47kJ
1000
(ii)Experiment II
Enthalpy change of CuSO4 = mass of water(m) x c x ∆T
=>100cm3 x 4.2 x 1.5 oC = -0.63kJ
1000
(c)Calculate the molar enthalpy of solution CuSO4 .5H2O (s) form the results in (i)experiment I.
∆Hs = CuSO4.5H2O= ∆H => -1.47kJ = 29.4kJ
Number of Moles 0.05 moles
(ii)experiment II.
∆Hs = CuSO4= ∆H => -0.63kJ = 12.6kJ
Number of Moles 0.05 moles
(d) Using an energy level diagram, calculate the molar enthalpy change for the reaction:
CuSO4 .5H2O (s) -> CuSO4(s) + 5H2O(l)
Energy cycle diagram
CuSO4(s) + (aq) + 5H2O(l) ∆H1=x CuSO4. 5H2O (s)+ (aq)
∆H3= =-29.4kJ ∆H2= -12.6kJ
CuSO4 .5H2O (aq)
∆H3 = ∆H1 +∆H2
=>-29.4kJ = -12.6kJ + x
=>-29.4kJ – (+12.6kJ) = x
x = 16.8kJ
b)Practical example II
Determination of enthalpy of solution of ammonium chloride
Theoretical information.
Ammonium chloride dissolves in water to form ammonium chloride solution. Aqueous ammonia can react with excess dilute hydrochloric acid to form ammonium chloride solution. The heat change taking place can be calculated from the heat of reactions:
(i) NH3(aq) + HCl(aq) -> NH4Cl(s)
(ii) NH4Cl(s) + (aq) -> NH4Cl(aq)
(iii) NH3(aq) + HCl(aq) -> NH4Cl(aq)
Experiment procedure I
Measure 50cm3 of water into a 100cm3 beaker. Record its temperature T1 as initial temperature to the nearest 0.5oC in table I. Add exactly 5.0g of ammonium chloride crystals weighed carefully into the water. Stir and record the highest temperature change T2 as the final temperature change. Repeat the above procedure to complete table I.
Sample results TableI
| Experiment | I | II |
| final temperature(oC) | 19.0 | 20.0 |
| initial temperature(oC) | 22.0 | 22.0 |
| temperature change ∆T(oC) | 3.0 | 2.0 |
Experiment procedure II
Measure 25cm3 of 2M aqueous ammonia into a 100cm3 beaker. Record its temperature T1 as initial temperature to the nearest 0.5oC in table II. Measure 25cm3 of 2M hydrochloric acid solution. Add the acid into the beaker containing aqueous ammonia. Stir and record the highest temperature change T2 as the final temperature change. Repeat the above procedure to complete table II.
Sample results:Table II
| Experiment | I | II |
| final temperature(oC) | 29.0 | 29.0 |
| initial temperature(oC) | 22.0 | 22.0 |
| temperature change ∆T(oC) | 7.0 | 7.0 |
Sample Calculations:
(a)Calculate the average ∆T in
(i)Table I
∆T= T2 -T1 => -3.0 +-2.0 = 2.5 oC
2
(ii)Table II
∆T= T2 -T1 => 7.0 +7.0 = 7.0 oC
2
(b)Calculate the enthalpy change for the reaction in:
(i)Experiment I
Enthalpy change ∆H = mass of Water(m) x c x ∆T
=>50cm3 x 4.2 x 2.5 oC = +0.525kJ
1000
(ii)Experiment II
Enthalpy change of CuSO4 = mass of water(m) x c x ∆T
=>25+25cm3 x 4.2 x 7 oC = +1.47kJ
1000
(c)Write the equation for the reaction taking place in:
(i)Experiment I
NH4Cl(s) + (aq) -> NH4Cl(aq)
(ii)Experiment I
NH3(aq) + HCl(aq) -> NH4Cl(aq)
(d)Calculate the enthalpy change ∆H for the reaction:
NH3(g) + HCl(g) -> NH4Cl(s) given that:
(i) NH3(g) + (aq) -> NH3(aq) ∆H= -40.3kJ
(ii) (aq) + HCl(g) -> HCl(aq) ∆H= -16.45kJ
(e)Applying Hess’ Law of constant heat summation:
Energy level diagram
N2(g) + 1½ H2(g) + ½ Cl2 ∆Hf NH4Cl(s) + aq
+0.525kJ=∆H4
(aq) (aq)
– 40.3kJ=∆H1 -16.43kJ=∆H2
NH3 (aq) + HCl(aq) -1.47kJ=∆H3 NH4Cl(s)
∆H1 + ∆H2 + ∆H3 = ∆H4 + ∆Hf
– 40.3kJ + -16.43kJ + -1.47kJ = +0.525kJ + ∆Hf
=>∆Hf = -58.865kJ.
Practice theoretical examples:
1. Using an energy level diagram calculate the ∆Hs of ammonium chloride crystals given that.
∆Hf of NH3 (aq) = -80.54kJ mole-1
∆Hf of HCl (aq) = -164.46kJ mole-1
∆Hf of NH4Cl (aq) = -261.7483kJ mole-1
∆Hs of NH4Cl (aq) = -16.8517kJ mole-1
N2(g) + 1½ H2(g) + ½ Cl2 ∆Hf=-261.7483kJ NH4Cl(s) + aq
x=∆Hs
(aq) (aq)
– 80.54kJ=∆H1 -164.46kJ=∆H2
NH3 (aq) + HCl(aq) 16.8517kJ=∆H3 NH4Cl(s)
∆H1 + ∆H2 + ∆H3 = ∆H4 + ∆Hf
– 80.54kJ + -164.46kJ + -16.8517kJ = -261.7483kJ + ∆Hf
=>∆Hf = -33.6kJmole-1.
Study the energy cycle diagram below and use it to:
∆H1 – enthalpy/heat of formation of sodium chloride (∆Hf)
∆H2 -enthalpy/heat of atomization of sodium (∆Hat)
∆H3 -enthalpy/heat of ionization/ionization energy of sodium (∆H i)
∆H4 -enthalpy/heat of atomization of chlorine (∆Hat)
∆H5 -enthalpy/heat of electron affinity of chlorine (∆He)
∆H6 enthalpy/heat of lattice/Lattice energy of sodium chloride(∆H l)
(b) Calculate ∆H1 given that ∆H2 =+108kJ , ∆H3=+500kJ, ∆H4 =+121kJ ,∆H5 =-364kJ and ∆H6 =-766kJ
Working:
∆H1 =∆H2 +∆H3 +∆H4 +∆H5 +∆H6
Substituting:
∆H1= +108kJ + +500kJ + +121kJ +-364kJ + -766kJ
∆H1= -401kJmole-1
(c) Given the that:
(i) Ionization energy of sodium = + 500kJmole-1
(ii)∆Hat of sodium = + 110kJmole-1
(iii) Electron affinity of chlorine = – 363kJmole-1
(iv)∆Hat of chlorine = + 120kJmole-1
(v) ∆Hf of sodium chloride = -411kJ , calculate the lattice energy of sodium chloride using an energy cycle diagram.
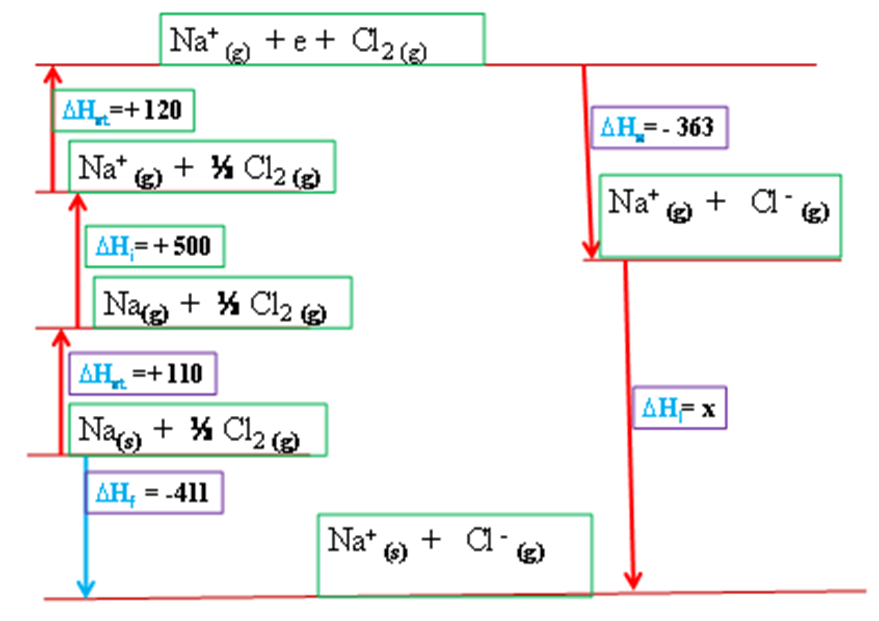
Working:
Applying Hess law then:
∆Hf =∆Ha +∆Hi +∆Ha +∆He +∆Hl
Substituting:
-411= +108kJ + +500kJ + +121kJ +-364kJ + x
-411 + -108kJ + -500kJ + -121kJ + +364kJ = x
x= -776kJmole-1
