The figure below shows the behaviour of emissions by a radioactive isotope x. Use it to answer the question follow
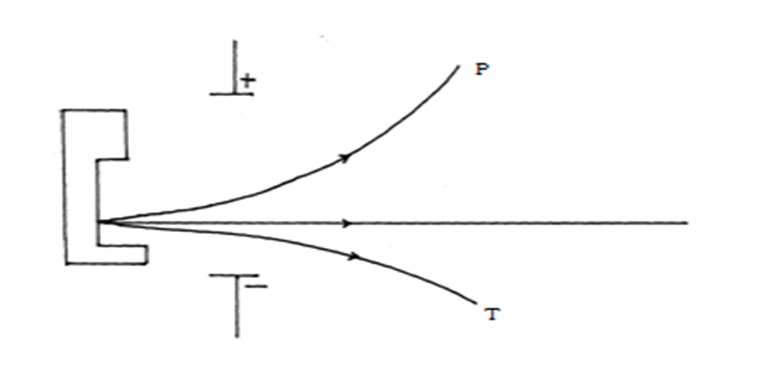
(a) Explain why isotope X emits radiations. (1mk)
-is unstable //has n/p ratio greater/less than one
(b) Name the radiation labeled T (1mk)
alpha particle
(c) Arrange the radiations labeled P and T in the increasing order of ability to be deflected by an electric filed. (1mk)
T -> P
a) Calculate the mass and atomic numbers of element B formed after 21280X has emitted three beta particles, one gamma ray and two alpha particles.
Mass number
= 212 – (0 beta+ o gamma + (2 x 4 ) alpha = 204
Atomic number
= 80 – (-1 x3) beta + 0 gamma + (2 x 2 )) alpha =79
b)Write a balanced nuclear equations for the decay of 21280X to B using the information in (a) above.
21280 X -> 20479B + 242He + 3 0-1e + y
Identify the type of radiation emitted from the following nuclear equations.
(i) 146C -> 147N + ………
β – Beta
- 11 H + 10n -> 21H + ……
y -gamma
(iii) 23592U -> 9542Mo + 13957La + 10n +……
7 β – seven beta particles
- 23892 U -> 23490Th + … …
α-alpha
- 146 C + 11H -> 157N + ……
y-gamma
X grams of a radioactive isotope takes 100 days to disintegrate to 20 grams. If the half-life period isotope is 25 days, calculate the initial mass X of the radio isotope.
Number of half-lifes = ( 100 / 25 ) = 4
20g —–> 40g —-> 80g—–> 160g —–> 320g
Original mass X = 320g
Radium has a half-life of 1620 years.
(i)What is half-life?
The half-life period is the time taken for a radioactive nuclide to spontaneously decay/ disintegrate to half its original mass/ amount
b)If one milligram of radium contains 2.68 x 10 18 atoms ,how many atoms disintegrate during 3240 years.
Number of half-lifes = ( 3240 / 1620 ) = 2
1 mg —1620—> 0.5mg —1620—-> 0.25mg
If 1mg -> 2.68 x 1018 atoms
Then 0.25 mg -> ( 0.25 x 2.68 x 1018 ) = 6.7 x 1017
Number of atoms remaining = 6.7 x 1017
Number of atoms disintegrated =
(2.68 x 1018 – 6.7 x 1017 )
= 2.01 x 1018
The graph below shows the mass of a radioactive isotope plotted against time
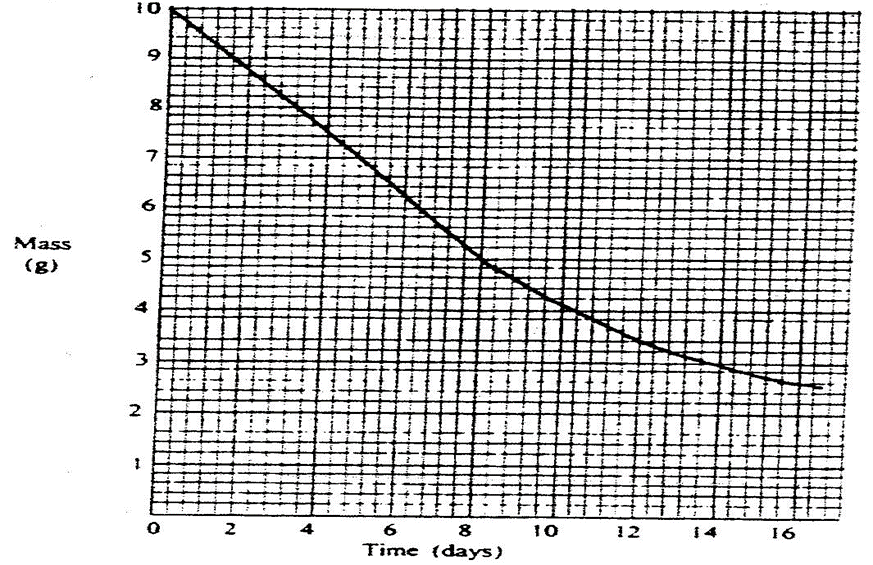
Using the graph, determine the half – life of the isotope
From graph 10 g to 5 g takes 8 days
From graph 5 g to 2.5 g takes 16 – 8 = 8 days
Calculate the mass of the isotope dacayed after 32 days
Number of half lifes= 32/8 = 4
Original mass = 10g
10g—1st –>5g—2nd–>2.5—3rd –>1.25—4th –>0.625 g
Mass remaining = 0.625 g
Mass decayed after 32 days = 10g – 0.625 g = 9.375g
A radioactive isotope X2 decays by emitting two alpha (a) particles and one beta (β) to form 214 83Bi
(a)Write the nuclear equation for the radioactive decay
21286X -> 214 83Bi + 242He + 0-1e
(b)What is the atomic number of X2?
86
(c) After 112 days, 1/16 of the mass of X2 remained. Determine the half life of X2
1—x-> 1 /2 –x-> 1 /4 –x-> 1 /8–x-> 1 /16
Number of t 1 /2 in 112 days = 4
t 1 /2 = 112 = 28 days
4
1.Study the nuclear reaction given below and answer the questions that follow.
126 C –step 1–>127 N –step 2–> 1211Na
(a)126 C and 146 C are isotopes. What does the term isotope mean?
Atoms of the same element with different mass number /number of neutrons.
(b)Write an equation for the nuclear reaction in step II
127 N -> 1211Na + 0 -1e
(c)Give one use of 146 C
Dating rocks/fossils:
Study of metabolic pathways/mechanisms on plants/animals
Study the graph of a radioactive decay series for isotope H below.
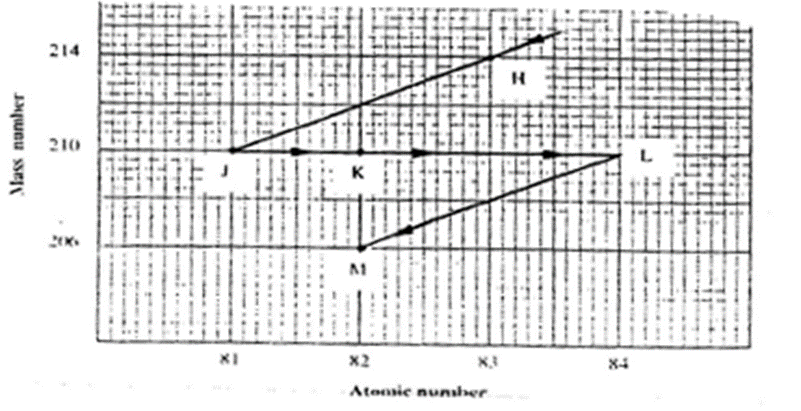
- Name the type of radiation emitted when isotope
(i) H changes to isotope J.
Alpha–Mass number decrease by 4 from 214 to 210(y-axis)
atomic number decrease by 2 from 83 to 81(x-axis)
(ii) J changes to isotope K
Beta–Mass number remains 210(y-axis)
atomic number increase by 1 from 81 to 82(x-axis).
(b) Write an equation for the nuclear reaction that occur when isotope
(i)J changes to isotope L
21081 J -> 21084L + 3 0 -1e
(i)H changes to isotope M
21483 H -> 20682M + 3 0 -1e + 2 4 2He
Identify a pair of isotope of an element in the decay series
K and M
Have same atomic number 82 but different mass number K-210 and M-206
a)A radioactive substance emits three different particles.
Identify the particle:
(i)with the highest mass.
Alpha/ α
(ii) almost equal to an electron
Beta/ β
1.a)State two differences between chemical and nuclear reactions(2mks)
(i) Nuclear reactions mainly involve protons and neutrons in the nucleus of an atom.Chemical reactions mainly involve outer electrons in the energy levels an atom.
(ii) Nuclear reactions form a new element. Chemical reactions do not form new elements
(iii) Nuclear reactions mainly involve evolution/production of large quantity of heat/energy.Chemical reactions produce or absorb smaller quantity of heat/energy.
(iv)Nuclear reactions are accompanied by a loss in mass /mass defect.
Chemical reactions are not accompanied by a loss in mass.
(v)Rate of decay/ disintegration of nuclide is independent of physical conditionsThe rate of a chemical reaction is dependent on physical conditions of temperature/pressure/purity/particle size/ surface area
b)Below is a radioactive decay series starting from 21483 Bi and ending at 20682 Pb. Study it and answer the question that follows.
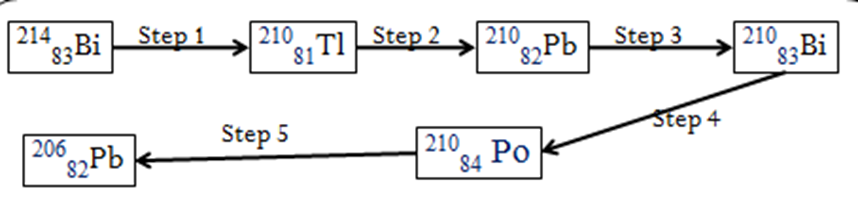
Identify the particles emitted in steps I and III (2mks)
I – α-particle
III – β-ray
ii)Write the nuclear equation for the reaction which takes place in (a) step I
21483Bi -> 21081Bi + 4 2 He
(b) step 1 to 3
21483Bi -> 21081Bi + 4 2 He + 2 0 -1 e
(c) step 3 to 5
21082Pb -> 20682Pb + 4 2 He + 2 0 -1 e
(c) step 1 to 5
21483Bi -> 20682Pb + 2 4 2 He + 3 0 -1 e
The table below give the percentages of a radioactive isotope of Bismuth that remains after decaying at different times.
| Time (min) | 0 | 6 | 12 | 22 | 38 | 62 | 100 |
| Percentage of Bismuth | 100 | 81 | 65 | 46 | 29 | 12 | 3 |
i)On the grid below , plot a graph of the percentage of Bismuth remaining(Vertical axis) against time.
ii)Using the graph, determine the:
I. Half – life of the Bismuth isotope
II. Original mass of the Bismuth isotope given that the mass that remained after 70 minutes was 0.16g (2mks)
d) Give one use of radioactive isotopes in medicine (1mk)
14.a)Distinguish between nuclear fission and nuclear fusion. (2mks)
Describe how solid wastes containing radioactive substances should be disposed of. (1mk)
b)(i)Find the values of Z1 and Z2 in the nuclear equation below
Z1 1 94 140 1
U + n -> Sr + Xe + 2 n
92 0 38 Z2 0
iii)What type of nuclear reaction is represented in b (i) above?
A radioactive cobalt 6128Co undergoes decay by emitting a beta particle and forming Nickel atom,
Write a balanced decay equation for the above change 1 mark
If a sample of the cobalt has an activity of 1000 counts per minute, determine the time it would take for its activity to decrease to 62.50 if the half-life of the element is 30years 2 marks
Define the term half-life. The diagram below shows the rays emitted by a radioactive sample

- Identify the rays S,R and Q
S- Beta ( β )particle/ray
R- Alpha (α )particle/ray
Q- Gamma (y )particle/ray
b) State what would happen if an aluminium plate is placed in the path of ray R,S and Q:
R-is blocked/stopped/do not pass through
Q-is not blocked/pass through
S-is blocked/stopped/do not pass through
(c)The diagram bellow is the radioactive decay series of nuclide A which is 24194Pu.Use it to answer the questions that follow. The letters are not the actual symbols of the elements.
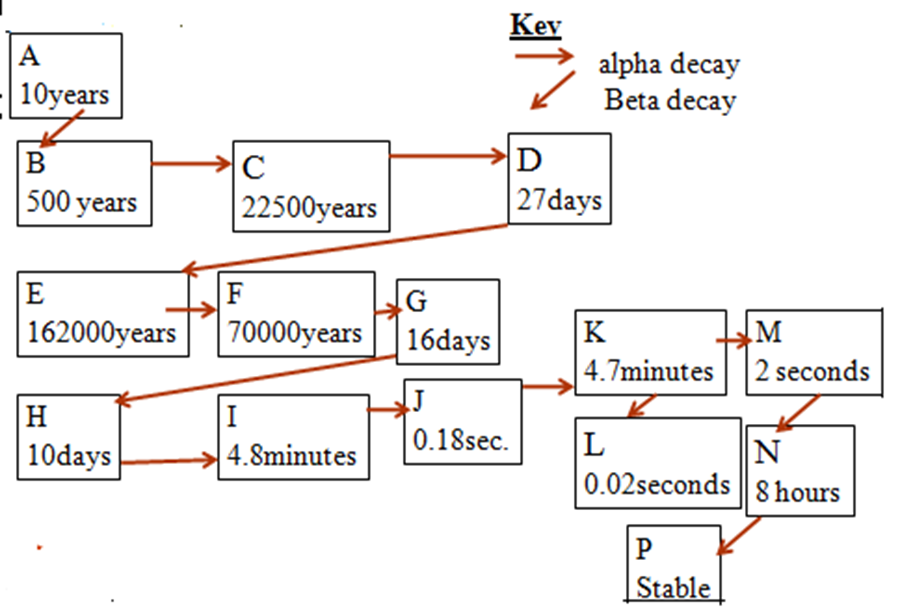
(a)Which letter represent the : Explain.
(i)shortest lived nuclide
L-has the shortest half life
(ii)longest lived nuclide
P-Is stable
(iii) nuclide with highest n/p ratio
L-has the shortest half life thus most unstable thus easily/quickly decay/disintegrate
(iv) nuclide with lowest n/p ratio
P-is stable thus do not decay/disintegrate
(b)How long would it take for the following:
(i)Nuclide A to change to B
10 years (half life of A)
(ii) Nuclide D to change to H
27days +162000years+70000years+16days
232000 years and 43 days
(iii) Nuclide A to change to P
27days +162000years+70000years+16days
232000 years and 43 days
Study
