RADIOACTIVITY-INTRODUCTION / CAUSES OF RADIOCTIVITY

Radioactivity is the spontaneous disintegration/decay of an unstable nuclide.

A nuclide is an atom with defined mass number (number of protons and neutrons), atomic number and definite energy.

Radioactivity takes place in the nucleus of an atom unlike chemical reactions that take place in the energy levels involving electrons.

A nuclide is said to be stable if its neutron: proton ratio is equal to one (n/p = 1)

All nuclide therefore try to attain n/p = 1 by undergoing radioactivity.

Examples

(i)Oxygen nuclide with ¹⁶₈ O has 8 neutrons and 8 protons in the nucleus therefore an n/p = 1 thus stable and do not decay/disintegrate.

(ii)Chlorine nuclide with ³⁵₁₇ Cl has 18 neutrons and 17 protons in the nucleus therefore an n/p = 1.0588  thus unstable and decays/disintegrates to try to attain n/p = 1.

(ii)Uranium nuclide with ²³⁷₉₂ U has 206 neutrons and 92 protons in the nucleus therefore an n/p = 2.2391 thus more unstable than  ²³⁵₉₂ U and thus more readily decays / disintegrates to try to attain n/p = 1.

(iii) Chlorine nuclide with ³⁷₁₇ Cl has 20 neutrons and 17 protons in the nucleus therefore an n/p = 1.1765 thus more unstable than  ³⁵₁₇ Cl and thus more readily decays / disintegrates to try to attain n/p = 1.

(iv)Uranium nuclide with ²³⁵₉₂ U has 143 neutrons and 92 protons in the nucleus therefore an n/p = 1.5543 thus more stable than  ²³⁷ ₉₂U  but also readily decays / disintegrates to try to attain n/p = 1.

All unstable nuclides naturally try to attain nuclear stability with the production of:

(i)alpha(α) particle decay

 The alpha (α) particle has the following main characteristic:

i)is positively charged(like protons)

ii) has mass number 4 and atomic number 2 therefore equal to a charged Helium atom ( ⁴₂He²⁺)

iii) have very low penetrating power and thus can be stopped /blocked/shielded by a thin sheet of paper.

iv) have high ionizing power thus cause a lot of damage to living cells.

v) a nuclide undergoing α-decay has its mass number reduced by 4 and its atomic number reduced by 2

Examples of alpha decay

²¹⁰ ₈₄ Pb                ->      ^x ₈₂ Pb         +       ⁴₂He ²⁺

²¹⁰ ₈₄ Pb               ->      ²⁰⁶ ₈₂ Pb      +       ⁴₂He ²⁺

²²⁶ ₈₈ Ra                ->      ²²² _y Rn       +       ⁴₂He ²⁺

²²⁶ ₈₈ Ra               ->      ²²² ₈₆ Rn      +       ⁴₂He ²⁺

  ^x _y U                    ->      ²³⁴₉₀ Th       +       ⁴₂He ²⁺

²³⁸ ₉₂ U                  ->      ²³⁴₉₀ Th       +       ⁴₂He ²⁺

^x _y U                     ->      ²³⁰₈₈ Ra       +       2 ⁴₂He ²⁺

²³⁸  ₉₂ U                 ->      ²³⁰₈₈ Ra       +       2 ⁴₂He ²⁺

  ²¹⁰ ₈₄ U                ->      ^x_y W            +        10 α

²¹⁰ ₈₄ U                  ->      ¹⁷⁰₆₄ W        +        10 α

  ²¹⁰  ₉₂U                ->      ^x_y W            +        6 α

²¹⁰  ₉₂U                  ->      ¹⁸⁶₈₀W        +        6 α

(ii)Beta (β) particle decay

The Beta (β) particle has the following main characteristic:

i)is negatively charged(like electrons)

ii)has  no mass number  and atomic number  negative one(-1)  therefore equal to a fast moving electron (⁰ _-1e)

iii) have medium  penetrating power and thus can be stopped /blocked/shielded by a thin sheet of  aluminium foil.

iv) have medium  ionizing power thus cause  less  damage to living cells than the α particle.

v) a nuclide undergoing β -decay has its mass number remain the same  and its atomic number increase by 1

Examples of beta (β) decay

1.²³ x Na              ->       ²³₁₂Mg                 +       ⁰ _-1e

 ²³ 11 Na               ->       ²³₁₂Mg                 +       ⁰ _-1e

 2. ²³⁴ x Th            ->       ^y₉₁ Pa                            +       ⁰ _-1e

       ²³⁴ 90 Th                   ->       ^y₉₁ Pa                  +       ⁰ _-1e

 3. ²⁰⁷₇₀Y              ->       x _y Pb                  +       3⁰ _-1e

      ²⁰⁷₇₀Y               ->       ²⁰⁷ ₇₃Pb               +       3⁰ _-1e

 4.x _yC                 ->         ¹⁴₇N                   +       ⁰ _-1e

       14 ₆C               ->         ¹⁴₇N                   +       ⁰ _-1e

 5. ¹ xn                 ->         ^y₁H                    +       ⁰ _-1e

   ¹ 0n                             ->         ¹₁H                              +       ⁰ _-1e

6. ⁴₂He                   ->      4¹₁H                    +        x ⁰ _-1e

     ⁴₂He                 ->      4¹₁H                     +         2 ⁰ _-1e

7. ²²⁸₈₈Ra              ->      ²²⁸₉₀Th                  +        x β

       ²²⁸₈₈Ra             ->       ²²⁸₉₂Th                +        4 β

 8.    ²³²₉₀Th                      ->     ²¹²₈₂Pb                  +       2 β     +        x α

                   ²³²₉₀Th        ->     ²¹²₈₂Pb                +       2 β    +        5 α

 9.  ²³⁸₉₂U               ->     ²²⁶₈₈ Ra                 +       x β      +      3 α

     ²³⁸₉₂U               ->       ²²⁶₈₈ Ra               +       2 β     +      3 α

10.  ²¹⁸₈₄Po             ->     ²⁰⁶₈₂Pb                  +       x β     +      3 α

      ²¹⁸₈₄Po            ->      ²⁰⁶₈₂Pb                 +       4β        +     3 α

(iii)Gamma (y) particle decay

The gamma (y) particle has the following main characteristic:

i)is neither negatively charged(like electrons/beta) nor positively charged(like protons/alpha) therefore neutral.

ii)has  no mass number  and atomic number therefore equal to   electromagnetic waves.

iii) have very high  penetrating power and thus can be stopped /blocked/shielded by a thick block of lead..

iv) have very low ionizing power thus cause  less  damage to living cells  unless on prolonged exposure..

v) a nuclide undergoing  y -decay has its  mass numberand its atomic number remain the same.

Examples of gamma (y) decay

• ³⁷₁₇Cl      ->            ³⁷₁₇Cl                  +         y
• ¹⁴₆C        ->            ¹⁴₆C           +         y

The sketch diagram below shows the penetrating power of the radiations from a radioactive nuclide.

radioactive nuclide      sheet of paper       aluminium foil       thick block of lead

(radiation source)          (block α-rays)         (block β-rays)          block y-rays)

                                                                                                                                                                                                                                                                                      α-rays                    β-rays                  y-rays

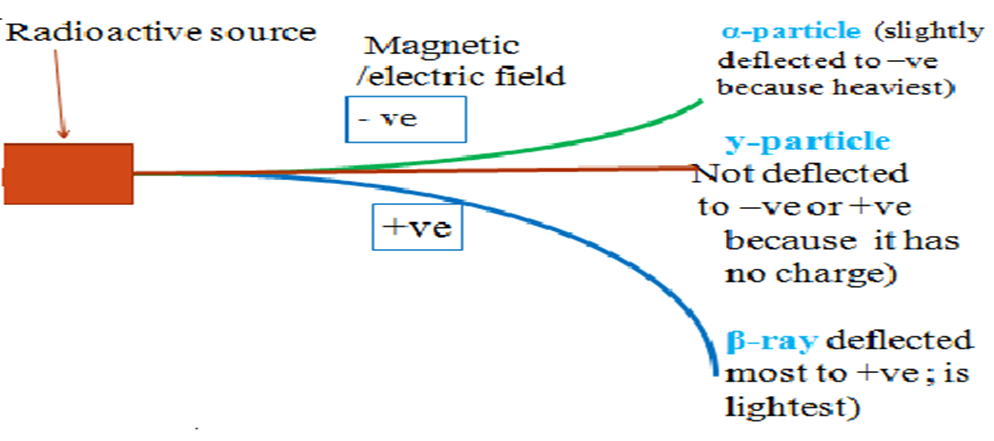
The sketch diagram below illustrates the effect of electric /magnetic field on the three radiations from a radioactive nuclide

Radioactive disintegration/decay naturally produces the stable ²⁰⁶₈₂Pb nuclide /isotope of lead.Below is the ²³⁸ ₉₂ U natural decay series. Identify the particle emitted in each case

Write the nuclear equation for the disintegration from :

(i)²³⁸ ₉₂ U   to       ²³⁴₉₀ T

          ²³⁸ ₉₂ U           ->         ²³⁴₉₀ T      +              ⁴ ₂ He ²⁺

           ²³⁸ ₉₂ U          ->         ²³⁴₉₀ T      +              α

(ii)²³⁸ ₉₂ U   to   ²²² ₈₄ Rn

 ²³⁸ ₉₂ U       ->         ²²²₈₄ Rn   +             4 ⁴ ₂ He ²⁺

  ²³⁸ ₉₂ U      ->         ²²²₈₄ Rn    +              4α

 ²³⁰ ₉₀ Th undergoes alpha decay to²²² ₈₆ Rn. Find the number ofα particles emitted. Write the nuclear equation for the disintegration.

Working      

 ²³⁰ ₉₀ Th     ->       ²²² ₈₆ Rn     +              x ⁴ ₂ He

Method 1

Using mass numbers

          230             =     222   +    4 x          =>   4 x  = 230  – 222  =  8

                   x = 8 / 4  = 2 α

Using atomic numbers

          90       =   86   +     2 x          =>    2 x  = 90  –  86  =  4

                     x = 4 / 2  = 2 α

Nuclear equation

²³⁰ ₉₀ Th      ->       ²²² ₈₆ Rn    +              2 ⁴ ₂ He

 ²¹⁴ ₈₂ Pb undergoes beta decay to²¹⁴ ₈₄ Rn. Find the number ofβ particles emitted. Write the nuclear equation for the disintegration.

Working      

 ²¹⁴ ₈₂ Pb      ->       ²¹⁴ ₈₄ Rn     +              x ⁰ _-1 e

Using atomic numbers only

           82      =    84   –      x          =>     -x  =  82  –  84  =  -2

                     x     = 2 β

Nuclear equation

 ²¹⁴ ₈₂ Pb      ->       ²¹⁴ ₈₄ Rn     +              2 ⁰ _-1 e

²³⁸ ₉₂ U undergoes beta and alpha decay to²⁰⁶ ₈₂ Pb. Find the number ofβ  andαparticles emitted. Write the nuclear equation for the disintegration.

Working      

          ²³⁸ ₉₂ U           ->       ²⁰⁶ ₈₂ Pb     +     x ⁰ _-1 e +                 y ⁴ ₂ He

Using Mass numbers only

           238             =    206   +    4y    =>     4y  = 238  –   206  =  32

                y     =    32      =     8 α

                             4

Using atomic numbers only and substituting the 8 α(above)

 ²³⁸ ₉₂ U       ->       ²⁰⁶ ₈₂ Pb      +            8 ⁴ ₂ He   +     x ⁰ _-1 e

           92      =          82               +      16           +     – x

                       =>   92 –  (82  +  16)   = – x  

                              x     = 6  β

Nuclear equation

          ²³⁸ ₉₂ U           ->       ²⁰⁶ ₈₂ Pb     +     6 ⁰ _-1 e +                 8 ⁴ ₂ He

 ²⁹⁸ ₉₂ U undergoes alpha and beta decay to²¹⁴ ₈₃ Bi. Find the number of  α and β particles emitted. Write the nuclear equation for the disintegration.

Working      

         ²⁹⁸ ₉₂ U              ->    ²¹⁰ ₈₃ Bi    +                 x ⁴ ₂ He      +     y ⁰ _-1 e

Using Mass numbers only

  298    =   214   +    4x    => 4x  = 298  –   214  =  84

     y     =     84      =     21 α

                     4

Using atomic numbers only and substituting the 21 α (above)

 ²³⁸ ₉₂ U   -> ²¹⁴ ₈₃Bi        +     21 ⁴ ₂ He   +     y ⁰ _-1 e

           92   =    83         +                 42       +     – y

                 =>   92 –  (83  +  42)   = – x  

                   x     =      33  β

Nuclear equation

                ²⁹⁸ ₉₂ U  ->   ²¹⁰ ₈₃ Bi    +   21 ⁴ ₂ He    +   33 ⁰ _-1 e