Radioactive disintegration/decay can be initiated in an industrial laboratory through two chemical methods:
a) nuclear fission
b) nuclear fusion.
a)Nuclear fission
Nuclear fission is the process which a fast moving neutron bombards /hits /knocks a heavy unstable nuclide releasing lighter nuclide, three daughter neutrons and a large quantity of energy.
Nuclear fission is the basic chemistry behind nuclear bombs made in the nuclear reactors.
The three daughter neutrons becomes again fast moving neutron bombarding / hitting /knocking a heavy unstable nuclide releasing lighter nuclides, three more daughter neutrons each and a larger quantity of energy setting of a chain reaction
Examples of nuclear equations showing nuclear fission
10 n + 235 b U -> 9038Sr + c 54Xe + 310n + a
10 n + 2713Al -> 2813Al + y + a
10 n + 28aAl -> b11Na + 42 He
a0 n + 147N -> 14bC + 11H
10 n + 11H -> 21H + a
10 n + 235 92 U -> 95 42 Mo + 139 57 La + 210n + 7 a
b) Nuclear fusion
Nuclear fusion is the process which smaller nuclides join together to form larger / heavier nuclides and releasing a large quantity of energy.
Very high temperatures and pressure is required to overcome the repulsion between the atoms.
Nuclear fusion is the basic chemistry behind solar/sun radiation.
Two daughter atoms/nuclides of Hydrogen fuse/join to form Helium atom/nuclide on the surface of the sun releasing large quantity of energy in form of heat and light.
21H + 21H -> abHe + 10n
21H + a -> 32He
21H + 21H -> a + 11H
4 11H -> 42He + a
147H + a -> 178O + 11H
C: HALF LIFE PERIOD (t1/2)
The half-life period is the time taken for a radioactive nuclide to spontaneously decay/ disintegrate to half its original mass/ amount.
It is usually denoted t 1/2.
The rate of radioactive nuclide disintegration/decay is constant for each nuclide.
The table below shows the half-life period of some elements.
| Element/Nuclide | Half-life period(t 1/2 ) |
| 238 92 U | 4.5 x 109 years |
| 14 6 C | 5600 years |
| 229 88 Ra | 1620 years |
| 35 15 P | 14 days |
| 210 84 Po | 0.0002 seconds |
The less the half life the more unstable the nuclide /element.
The half-life period is determined by using a Geiger-Muller counter (GM tube)
.A GM tube is connected to ratemeter that records the count-rates per unit time.
This is the rate of decay/ disintegration of the nuclide.
If the count-rates per unit time fall by half, then the time taken for this fall is the half-life period.
Examples
a)A radioactive substance gave a count of 240 counts per minute but after 6 hours the count rate were 30 counts per minute. Calculate the half-life period of the substance.
If t 1/2 = x
then 240 –x–>120 –x–>60 –x—>30
From 240 to 30 =3x =6 hours
=>x = t 1/2 = ( 6 / 3 )
= 2 hours
b) The count rate of a nuclide fell from 200 counts per second to 12.5 counts per second in 120 minutes.
Calculate the half-life period of the nuclide.
If t 1/2 =x
then
200 –x–>100 –x–>50 –x—>25 –x—>12.5
From 200 to 12.5 =4x =120 minutes
=>x = t 1/2 = ( 120 / 4 )
= 30 minutes
c) After 6 hours the count rate of a nuclide fell from 240 counts per second to 15 counts per second on the GM tube. Calculate the half-life period of the nuclide.
If t 1/2 = x
then 240 –x–>120 –x–>60 –x—>30 –x—>15
From 240 to 15 =4x =6 hours
=>x = t 1/2 = ( 6 / 4 )= 1.5 hours
d) Calculate the mass of nitrogen-13 that remain from 2 grams after 6 half-lifes if the half-life period of nitrogen-13 is 10 minutes.
If t 1/2 = x then:
2 —x–>1 –2x–>0.5 –3x—>0.25 –4x–>0.125–5x—>0.0625–6x—>0.03125
After the 6th half life 0.03125 g of nitrogen-13 remain.
e) What fraction of a gas remains after 1hour if its half-life period is 20 minutes?
If t 1/2 = x then:
then 60 /20 = 3x
1 –x–> 1/2 –2x–> 1/4 –3x—> 1/8
After the 3rd half-life 1/8 of the gas remain
f) 348 grams of a nuclide A was reduced to 43.5 grams after 270days.Determine the half-life period of the nuclide.
If t 1/2 = x then:
348 –x–>174 –2x–>87 –3x—>43.5
From 348 to 43.5=3x =270days
=>x = t 1/2 = ( 270 / 3 )
= 90 days
g) How old is an Egyptian Pharaoh in a tomb with 2grams of 14C if the normal 14C in a present tomb is 16grams.The half-life period of 14C is 5600years.
If t 1/2 = x = 5600 years then:
16 –x–>8 –2x–>4 –3x—>2
3x = ( 3 x 5600 )
= 16800years
h) 100 grams of a radioactive isotope was reduced 12.5 grams after 81days.Determine the half-life period of the isotope.
If t 1/2 = x then:
100 –x–>50 –2x–>25 –3x—>12.5
From 100 to 12.5=3x =81days
=>x = t 1/2
= ( 81 / 3 )
= 27 days
A graph of activity against time is called decay curve.
A decay curve can be used to determine the half-life period of an isotope since activity decrease at equal time interval to half the original
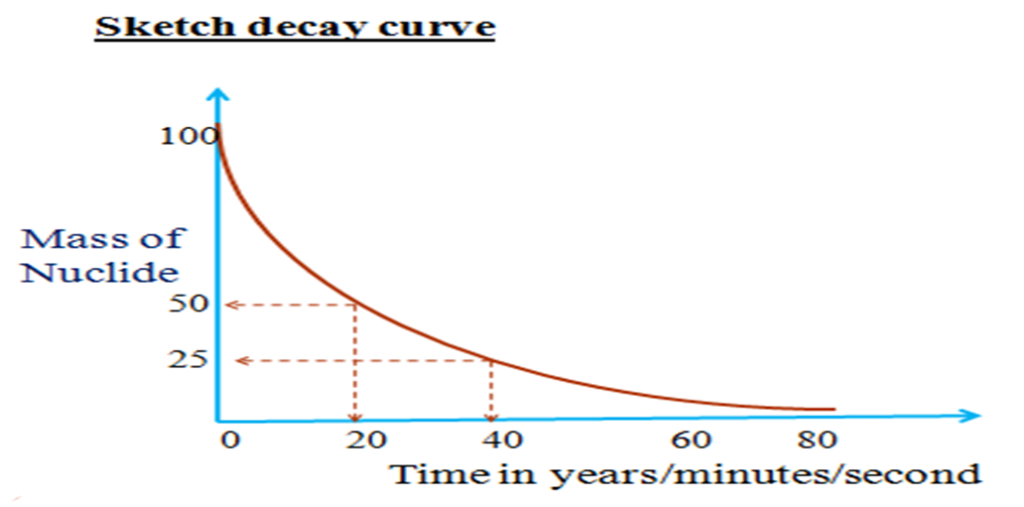
= 20 minutes
( 50 – 25 ) => ( 40 – 20 ) = 20 minutes
Thus t ½ = 20 minutes
(ii)Why does the graph tend to ‘O’?
Smaller particle/s will disintegrate /decay to half its original.
There can never be ‘O’/zero particles
