Maths Form 3 Past Paper Questions with Marking Scheme
3. A famer has a piece of land measuring 840m by 396m. He divides it into square plots of equal sizes. Find the maximum area of one plot. (3mks)
4. A tourist arrived in Kenya with sterling pound (£) 4680 all of which he exchanged into Kenyan money. He spent Ksh.51790 while in Kenya and converted the rest of the money into US dollars. Calculate the amount he received in US dollars. The. Exchange rates were as follows. (4mks)
Buying Selling
US dollars $ 65.20 69.10
Sterling pounds £ 123.40 131.80
5. The gradient of a straight line L1, passing through the point P (3, 4) and Q (a, b) is -3/2.
A line L2 is perpendicular to L1 through Q and R (2, -1). Determine the values of a and b. (3mks)
6. In Blessed Church Choir the ratio of males to females is 2:3. On one Sunday service ten male members were absent and six new female members joined the choir as guests for the day.
If on this day the ratio of males to females was 1:3, how many regular members does the
choir have? (3mks)
7. A businessman makes a profit of 20% when he sells a carpet for Ksh. 36000. In a trade fair he sold one such carpet for Ksh. 33600. Calculate the percentage profit made on the sale of the carpet during the trade fair. (3mks)
8. Use tables of logarithms to evaluate; (4mks)
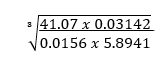

10. State all the integral values of x that satisfy the following inequality. (3mks)
2x-3≤3x+5≥7x+6
11. In the question use a pair of compasses and a ruler only.
(a) Construct triangle ABC such that AB=6cm, BC=8cm and <ABC=1350 (3mks)
(b) Construct the height of ABC in (a) above taking BC as the base. (1mk)
12. Without using mathematical tables or a calculator, evaluate. (3mks)
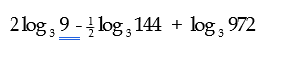
13. Use tables of reciprocals, squares and cube roots to evaluate the following (4mks)
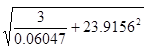
14. Jane spends 1/8 of her monthly salary on school fees and a third of the remainder on rent .
She spends 3/4 of what remains after paying school fees and rent on food. If she is left with Ksh.1470, calculate her monthly salary. (3mks)
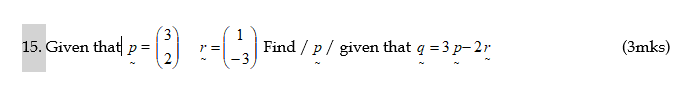
16. The dimensions of a rectangle are 10cm and 15cm. If there is an error of 5% in each of the measurements, find the maximum possible area of the rectangle. (3mks)
Form 3 Mathematics Questions SECTION II (50MKS)
17. Hellen’s earnings are as follows:
Basic salary sh. 38000 per month
House allowance sh. 14000 per months
Travelling allowance sh.8500 per month and
Medical allowance Ksh.3300 per month.
She is given a personal relief of Ksh. 12672
The table for payable tax is shown below

Calculate
(a) (i) Hellen’s taxable income in K£ p.a (2mks)
(ii) Her P.A.Y.E (5mks)
(b) Hellen is deducted the following items per month
NHIF Ksh.320
Cooperative shares Ksh.2000
Loan repayment Ksh5000
Determine her net salary per month (3mks)
18. Completer the table below for y=2x2-x-3 (2mks)
| x | -3 | -2 | -1 | 0 | 1 | 2 | 3 |
| 2x2 | 18 | 2 | 0 | 18 | |||
| -x | 3 | 1 | 0 | -3 | -2 | ||
| -3 | -3 | -3 | -3 | -3 | -3 | -3 | -3 |
| y | 18 | 7 | 3 | 12 |
(a) Draw the graph of y=2x2-x-3 for -3 ≤x≤3 (3mks)

(b) Using a suitable triangle line solve
(i) 2x2 -x-3=0 (1mk)
(ii) 2x2 – 3x-5=0 (2mks)
(iii) 2x2-2x-1=0 (2mks)
19. A group of people planned to contribute sh.2000 000 to start a business. However before the contributions were made the group disintegrated and 40 members pulled out. A a result each of the remaining members were to contribute sh. 2500 more
(a) Find the original number of members in the group. (5mks)
(b) After each member contributing half of the expected amount the members opted to
get a bank that would offset ¼ of the remaining amount. How much would each member contribute after he bank loan. (3mks)
(c) Twenty new members joined the group just before the business started. As a result the old members were to be refunded some money. How much was the refund? (2mks)
20. The figure below (not drawn to scale) shows a triangle ABC inscribed in a circle. AB=6cm, BC=9cm and AC=10cm
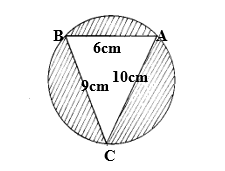
Calculate;
(a) The radius of the circle (5mks)
(b) The area of the shaded region. (5mks)
21. A Matatu and a Nissan left town A for town B 240km away at 8.00am travelling at a speed of 90km/hr and 120 km/h respectively. After 20minutes the Nissan had a puncture which took 30minutes to mend.
(a) How far from town A did the Nissan catch up with the Matatu? (6mks)
(b)At what time did the Nissan catch up with the Matatu? (1mk)
(c) At what time did the Matatu reach town B (3mks)
22. The diagram below shows a frustrum of a right circular cone. The radii of the circle at the top and the bottom are 1.5cm and 5cm respectively. The slant edge of the frustrum is 7cm long.
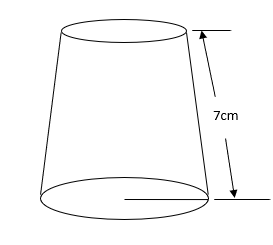
Calculate:
(a) The height of the frustrum. (4mks)
(b) The total surface area of the frustrum. (6mks)
23. Samatha and Meshi entered into a business partnership in which they contributed Kshs. 120,000 and Kshs. 150,000 every year respectively. After one year Fuki joined the business and contributed Kshs. 90,000
a) Calculate the ratio of their investment after 3 years of business (3mks)
b) It was agreed that 30% of the profits after 3 years be used to cater for the cost of running the business, while the remaining would be shared proportionally. Calculate each persons share if the profit made after three years was Kshs, 187,000. (4mks)
c) If each of them invested their shares in the business, find their new individual investments at the beginning of the fourth year. (3mks)
24. (a) A line, L1 passes through the points (3,3) and (5,7). Find the equation of L1 in the
form y = mx+c where m and c are constants. (3mks)
(b) Another line L2 is perpendicular to L1 and passes through (-2, 3). Find:
(i) The equation of L2; (2mks)
(ii) The x-intercept of L2. (2mks)
(c) Determine the point of intersection of L1 and L2. (3mks)
 Join Our WhatsApp Group
Join Our WhatsApp Group