Maths Form 4 Past Paper 2 Questions with Marking Scheme
SECTION I (50MKS)
1. Simplify by rationalising the denominator (3mks)
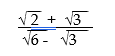
2. Find the value of x in the equation log10 (2x-1) + log10 3 = log10 (8x-1). (3mks)
3. Find the compound interest on sh. 200,000 for 2 years at 14% pa. Compounded
semi-annually. (3mks)
4. The ratio of 12th to 10th term in a geometric series is 9:1. Find the common ratio. (3mks)
5. i) Expand (2 – ¼ x)5 (2mks)
ii) Use your expansion to find the value of (1.96)5 correct to 3 decimal places (2mks)
6. Chord WX and YZ intersect externally at Q. The secant WQ = 11cm and QX = 6cm while
ZQ = 4cm.
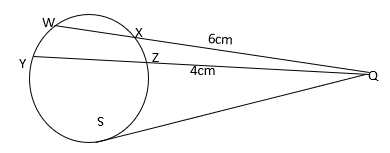
(a) Calculate the length of chord YZ. (2mks)
(b) Using the answer in (a) above, find the length of the tangent SQ. (2mks)
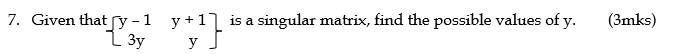
8. The masses to the nearest kg of 50 adults were recorded as follows:

Calculate the quartile deviation. (3mks)
9. P varies as the cube of Q and inversely as the square root of R. If Q is increased by 20% and R decreased by 36%, find the percentage change in P. (3mks)
10. Solve 8 cos2 x – 2 cos x – 1 = 0 (3mks)
11. Make c the subject of the formula:

12. The position vectors of A and B are given as a= 2i-3j+4k and b= -2i–j+2k respectively. Find
to 2decimal places, the length of the vector. (3mks)
13. Find the centre and the radius of a circle whose equation is
x2-6x+y2-10y+30=0 (3mks)
14. A point (x, y) is mapped onto (13, 13) by two transformations M followed by T where
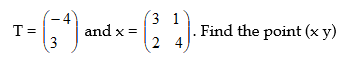
15. Given that 2 £ A £ 4 and 0.1 £ B £ 0.2. Find the minimum value of
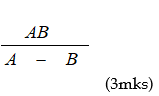
16. In a transformation, an object with area 9cm2 is mapped onto an image whose area is 54cm2. Given that the matrix of transformation is
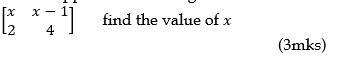
F4 Maths Questions SECTION II (50MKS)
17. The table below shows the rates of taxation in a certain year.
Income in K£ pa Rate in Ksh per K£
1 – 3900 2
3901 – 7800 3
7801 – 11700 4
11701 – 15600 5
15601 – 19500 7
Above 19500 9
In that period, Juma was earning a basic salary of sh. 21,000 per month. In addition, he
was entitled to a house allowance of sh. 9000 p.m. and a personal relief of ksh.105 p.m
He also has an insurance scheme for which he pays a monthly premium of sh. 2000. He
is entitled to a relief on premium at 15% of the premium paid.
(a) Calculate how much income tax Juma paid per month. (7mks)
(b) Juma’s other deductions per month were cooperative society contributions of sh. 2000
and a loan repayment of sh. 2500. Calculate his net salary per month. (3mks)
18. Wainaina has two dairy farm A and B. Farm A produces milk with 3 ½ percent fat and
farm B produces milk with 4 ¾ percent fat. Determine;
(a) The total mass of milk fat in 50kg of milk from farm A and 30kg from farm B. (3mks)
(b) The percentage of fat in a mixture of 50kg of milk from A and 30kg of milk from farm B. (2mks)
(c) Determine the range of values of mass of milk from farm B that must be used in a 50kg mixture so that the mixture may have at least 4 percent fat. (5mks)
19. A cupboard has 7 white cups and 5 brown ones all identical in size and shape. There
was a blackout in the town and Mrs. Kamau had to select three cups, one after the other
without replacing the previous one.
(a) Draw a tree diagram for the information. (2mks)
(b) Calculate the probability that she chooses.
(i) Two white cups and one brown cup. (2mks)
(ii) Two brown cups and one white cup. (2mks)
(iii) At least one white cup. (2mks)
(iv) Three cups of the same colour. (2mks)
20. (i) complete the table below, giving the values correct to 2 decimal places (2mks)
| X0 | 00 | 150 | 300 | 450 | 600 | 750 | 900 | 1050 | 1200 | 1350 | 1500 | 1650 | 1800 |
| Cos 2X0 | 1.00 | 0.87 | 0.00 | -0.5 | -1.00 | -0.5 | 0.00 | 0.50 | 0.87 | 1.00 | |||
| Sin (X0+300) | 0.50 | 0.71 | 0.87 | 0.97 | 1.00 | 0.87 | 0.71 | 0.50 | 0.00 | -0.50 |

(iii) Find the period of the curve y=cos 2x0 (1mk)
(iv) Using the graph, estimate the solutions to the equations;
(a) sin(X0+300)=cos 2X0 (1mk)
(b) Cos 2X0=0.5 (1mk)
21. The For a sample of 100 bulbs, the time taken for each bulb to burn was recorded. The table below shows the result of the measurements.
| Time(in hours) | 15-19 | 20-24 | 25-29 | 30-34 | 35-39 | 40-44 | 45-49 | 50-54 | 55-59 | 60-64 | 65-69 | 70-74 |
| Number of bulbs | 6 | 10 | 9 | 5 | 7 | 11 | 15 | 13 | 8 | 7 | 5 | 4 |
(a) Using an assumed mean of 42, calculate
(i) the actual mean of distribution (4mks)
(4mks)
(ii) the standard deviation of the distribution (3mks)
(b) Calculate the quartile deviation (3mks)
22. (a) Using a ruler and a pair of compasses only, construct a parallelogram ABCD such that
AB=9 cm, AD=7 cm and angle BAD=60o. (3mks)
(b) On the same diagram, construct:
(i) The locus of a point P such that P is equidistant from AB and AD; (1mk)
(ii) The locus of a point Q such that Q is equidistant from B and C; (1mk)
(iii) The locus of a point T such that T is equidistant from AB and DC; (1mk).
(c) (i) Shade the region R bounded by the locus of P, the locus of Q and the locus of T. (1mk)
(ii) Find the area of the region shaded in (d)(i) above. (3mks)
23. The points A (1,4), B(-2,0) and C (4,-2) of a triangle are mapped onto A1(7,4), B1(x,y) and
C1 (10,16) by a transformation N = . Find
(i) Matrix N of the transformation (4mks)
(ii) Coordinates of B1 (2mks)
(iii) AIIBIICII are the image of A1B1C1 under transformation represented by matrix
M = Write down the co-ordinates of AIIBIICII (2mks)
(vi)A transformation N followed by M can be represented by a single transformation K.
Determine K (2mks)
24. The roof of a ware house is in the shape of a triangular prism as shown below
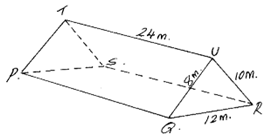
Calculate
(a) The angle between faces RSTU and PQRS (3mks)
(b) The space occupied by the roof (3mks)
(c) The angle between the plane QTR and PQRS (4mks)
 Join Our WhatsApp Group
Join Our WhatsApp Group