1.The empirical formula of a compound is its simplest formula. It is the simplest whole number ratios in which atoms of elements combine to form the compound. 2.It is mathematically the lowest common multiple (LCM) of the atoms of the elements in the compound
3.Practically the empirical formula of a compound can be determined as in the following examples.
To determine the empirical formula of copper oxide
(a)Method 1:From copper to copper(II)oxide
Procedure.
Weigh a clean dry covered crucible(M1).Put two spatula full of copper powder into the crucible. Weigh again (M2).Heat the crucible on a strong Bunsen flame for five minutes. Lift the lid, and swirl the crucible carefully using a pair of tong. Cover the crucible and continue heating for another five minutes. Remove the lid and stop heating. Allow the crucible to cool. When cool replace the lid and weigh the contents again (M3).
Sample results
| Mass of crucible(M1) | 15.6g |
| Mass of crucible + copper before heating(M2) | 18.4 |
| Mass of crucible + copper after heating(M3) | 19.1 |
Sample questions
1. Calculate the mass of copper powder used.
Mass of crucible + copper before heating(M2) = 18.4
Less Mass of crucible(M1) = – 15.6g
Mass of copper 2.8 g
2. Calculate the mass of Oxygen used to react with copper.
Method I
Mass of crucible + copper after heating(M3) = 19.1g
Mass of crucible + copper before heating(M2) = – 18.4g
Mass of Oxygen = 0.7 g
Method II
Mass of crucible + copper after heating(M3) = 19.1g
Mass of crucible = – 15.6g
Mass of copper(II)Oxide = 3.5 g
Mass of copper(II)Oxide = 3.5 g
Mass of copper = – 2.8 g
Mass of Oxygen = 0.7 g
3. Calculate the number of moles of:
(i) copper used (Cu = 63.5)
number of moles of copper = mass used => 2.8 = 0.0441moles
Molar mass 63.5
(ii) Oxygen used (O = 16.0)
number of moles of oxygen = mass used => 0.7 = 0.0441moles
Molar mass 16.0
4. Determine the mole ratio of the reactants
Moles of copper = 0.0441moles = 1 => Mole ratio Cu: O = 1:1
Moles of oxygen 0.0441moles 1
5.What is the empirical, formula of copper oxide formed.
CuO (copper(II)oxide
6. State and explain the observations made during the experiment.
Observation
Colour change from brown to black
Explanation
Copper powder is brown. On heating it reacts with oxygen from the air to form black copper(II)oxide
7. Explain why magnesium ribbon/shavings would be unsuitable in a similar experiment as the one above.
Hot magnesium generates enough heat energy to react with both Oxygen and Nitrogen in the air forming a white solid mixture of Magnesium oxide and magnesium nitride. This causes experimental mass errors.
(b)Method 2:From copper(II)oxide to copper
Procedure.
Weigh a clean dry porcelain boat (M1). Put two spatula full of copper(II)oxide powder into the crucible. Reweigh the porcelain boat (M2).Put the porcelain boat in a glass tube and set up the apparatus as below;
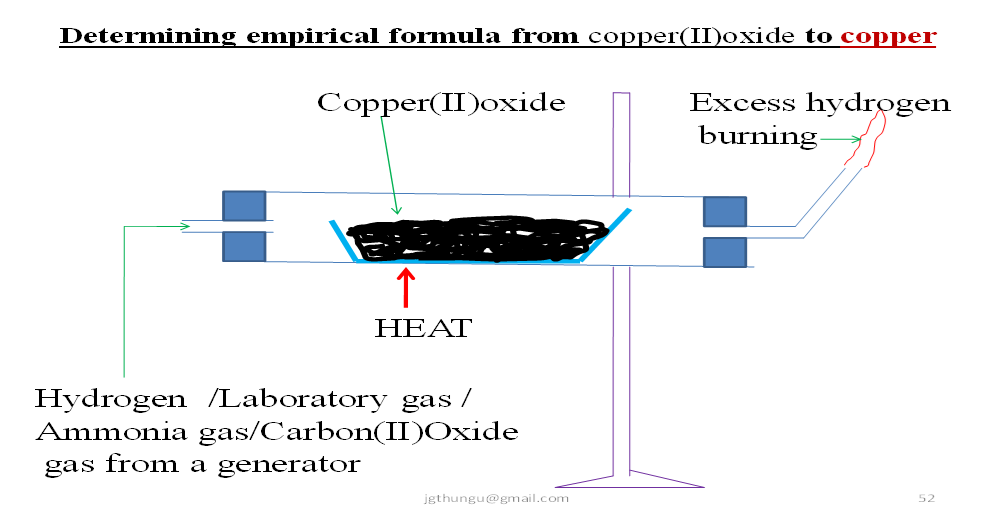
Pass slowly(to prevent copper(II)oxide from being blown away)a stream of either dry Hydrogen /ammonia/laboratory gas/ carbon(II)oxide gas for about two minutes from a suitable generator.
When all the in the apparatus set up is driven out ,heat the copper(II)oxide strongly for about five minutes until there is no further change. Stop heating.
Continue passing the gases until the glass tube is cool.
Turn off the gas generator.
Carefully remove the porcelain boat form the combustion tube.
Reweigh (M3).
Sample results
| Mass of boat(M1) | 15.6g |
| Mass of boat before heating(M2) | 19.1 |
| Mass of boat after heating(M3) | 18.4 |
Sample questions
1. Calculate the mass of copper(II)oxide used.
Mass of boat before heating(M2) = 19.1
Mass of empty boat(M1) = – 15.6g
Mass of copper(II)Oxide 3.5 g
2. Calculate the mass of
(i) Oxygen.
Mass of boat before heating(M2) = 19.1
Mass of boat after heating (M3) = – 18.4g
Mass of oxygen = 0.7 g
(ii)Copper
Mass of copper(II)Oxide = 3.5 g
Mass of oxygen = 0.7 g
Mass of oxygen = 2.8 g
3. Calculate the number of moles of:
(i) Copper used (Cu = 63.5)
number of moles of copper = mass used => 2.8 = 0.0441moles
Molar mass 63.5
(ii) Oxygen used (O = 16.0)
number of moles of oxygen = mass used => 0.7 = 0.0441moles
Molar mass 16.0
4. Determine the mole ratio of the reactants
Moles of copper = 0.0441moles = 1 => Mole ratio Cu: O = 1:1
Moles of oxygen 0.0441moles 1
5.What is the empirical, formula of copper oxide formed.
CuO (copper(II)oxide
6. State and explain the observations made during the experiment.
Observation
Colour change from black to brown
Explanation
Copper(II)oxide powder is black. On heating it is reduced by a suitable reducing agent to brown copper metal.
7. Explain why magnesium oxide would be unsuitable in a similar experiment as the one above.
Magnesium is high in the reactivity series. None of the above reducing agents is strong enough to reduce the oxide to the metal.
8. Write the equation for the reaction that would take place when the reducing agent is:
(i) Hydrogen
CuO(s) + H2(g) -> Cu(s) + H2O(l)
(Black) (brown) (colourless liquid form
on cooler parts )
(ii)Carbon(II)oxide
CuO(s) + CO (g) -> Cu(s) + CO2(g)
(Black) (brown) (colourless gas, form
white ppt with lime water )
(iii)Ammonia
3CuO(s) + 2NH3(g) -> 3Cu(s) + N2 (g) + 3H2O(l)
(Black) (brown) (colourless liquid form
on cooler parts )
9. Explain why the following is necessary during the above experiment;
(i)A stream of dry hydrogen gas should be passed before heating copper (II) Oxide.
Air combine with hydrogen in presence of heat causing an explosion
(ii)A stream of dry hydrogen gas should be passed after heating copper (II) Oxide has been stopped.
Hot metallic copper can be re-oxidized back to copper(II)oxide
(iii) A stream of excess carbon (II)oxide gas should be ignited to burn
Carbon (II)oxide is highly poisonous/toxic. On ignition it burns to form less toxic carbon (IV)oxide gas.
10. State two sources of error in this experiment.
(i)All copper(II)oxide may not be reduced to copper.
(ii)Some copper(II)oxide may be blown out the boat by the reducing agent.
4.Theoreticaly the empirical formula of a compound can be determined as in the following examples.
(a)A oxide of copper contain 80% by mass of copper. Determine its empirical formula. (Cu = 63.5, 16.0)
% of Oxygen = 100% – % of Copper => 100- 80 = 20% of Oxygen
| Element | Copper | Oxygen |
| Symbol | Cu | O |
| Moles present = % composition Molar mass | 80 63.5 | 20 16 |
| Divide by the smallest value | 1.25 1.25 | 1.25 1.25 |
| Mole ratios | 1 | 1 |
Empirical formula is CuO
(b)1.60g of an oxide of Magnesium contain 0.84g by mass of Magnesium. Determine its empirical formula(Mg = 24.0, 16.0)
Mass of Oxygen = 1.60 – 0.84 => 0.56 g of Oxygen
| Element | Magnesium | Oxygen |
| Symbol | Mg | O |
| Moles present = % composition Molar mass | 0.84 24 | 0.56 16 |
| Divide by the smallest value | 0.35 0.35 | 0.35 0.35 |
| Mole ratios | 1 | 1 |
Empirical formula is MgO
(c)An oxide of Silicon contain 47% by mass of Silicon. What is its empirical formula(Si = 28.0, 16.0)
Mass of Oxygen = 100 – 47 => 53% of Oxygen
| Element | Silicon | Oxygen |
| Symbol | Si | O |
| Moles present = % composition Molar mass | 47 28 | 53 16 |
| Divide by the smallest value | 1.68 1.68 | 3.31 1.68 |
| Mole ratios | 1 | 1.94 = 2 |
Empirical formula is SiO2
(d)A compound contain 70% by mass of Iron and 30% Oxygen. What is its empirical formula(Fe = 56.0, 16.0)
Mass of Oxygen = 100 – 47 => 53% of Oxygen
| Element | Silicon | Oxygen |
| Symbol | Si | O |
| Moles present = % composition Molar mass | 47 28 | 53 16 |
| Divide by the smallest value | 1.68 1.68 | 3.31 1.68 |
| Mole ratios | 1 | 1.94 = 2 |
Empirical formula is SiO2
2.During heating of a hydrated copper (II)sulphate(VI) crystals, the following readings were obtained:
Mass of evaporating dish =300.0g
Mass of evaporating dish + hydrated salt = 305.0g
Mass of evaporating dish + anhydrous salt = 303.2g
Calculate the number of water of crystallization molecules in hydrated copper (II)sulphate(VI)
(Cu =64.5, S = 32.0,O=16.0, H = 1.0)
Working
Mass of Hydrated salt = 305.0g -300.0g = 5.0g
Mass of anhydrous salt = 303.2 g -300.0g = 3.2 g
Mass of water in hydrated salt = 5.0g -3.2 g = 1.8g
Molar mass of water(H2O) = 18.0g
Molar mass of anhydrous copper (II)sulphate(VI) (CuSO4) = 160.5g
| Element/compound | anhydrous copper (II) sulphate(VI) | Oxygen |
| Symbol | CuSO4 | O |
| Moles present = composition by mass Molar mass | 3,2 160.5 | 1.8 18 |
| Divide by the smallest value | 0.0199 0.0199 | 0.1 18 |
| Mole ratios | 1 | 5 |
The empirical formula of hydrated salt = CuSO4.5H2O
Hydrated salt has five/5 molecules of water of crystallizations
4. The molecular formula is the actual number of each kind of atoms present in a molecule of a compound.
The empirical formula of an ionic compound is the same as the chemical formula but for simple molecular structured compounds, the empirical formula may not be the same as the chemical formula.
The molecular formula is a multiple of empirical formula .It is determined from the relationship:
(i) n = Relative formular mass
Relative empirical formula
where n is a whole number.
(ii) Relative empirical formula x n = Relative formular mass where n is a whole number.
Practice sample examples
1. A hydrocarbon was found to contain 92.3% carbon and the remaining Hydrogen.
If the molecular mass of the compound is 78, determine the molecular formula(C=12.0, H =1.0)
Mass of Hydrogen = 100 – 92.3 => 7.7% of Oxygen
| Element | Carbon | Hydrogen |
| Symbol | C | H |
| Moles present = % composition Molar mass | 92.3 12 | 7.7 1 |
| Divide by the smallest value | 7.7 7.7 | 7.7 7.7 |
| Mole ratios | 1 | 1 |
Empirical formula is CH
The molecular formular is thus determined :
n = Relative formular mass = 78 = 6
Relative empirical formula 13
The molecular formula is (C H ) x 6 = C6H6
2. A compound of carbon, hydrogen and oxygen contain 54.55% carbon, 9.09% and remaining 36.36% oxygen.
If its relative molecular mass is 88, determine its molecular formula(C=12.0, H =1.0, O= 16.0)
| Element | Carbon | Hydrogen | Oxygen |
| Symbol | C | H | O |
| Moles present = % composition Molar mass | 54.55 12 | 9.09 1 | 36.36 16 |
| Divide by the smallest value | 4.5458 2.2725 | 9.09 2.2725 | 2.2725 2.2725 |
| Mole ratios | 2 | 4 | 1 |
Empirical formula is C2H4O
The molecular formula is thus determined :
n = Relative formular mass = 88 = 2
Relative empirical formula 44
The molecular formula is (C2H4O ) x 2 = C4H8O2.
4.A hydrocarbon burns completely in excess air to form 5.28 g of carbon (IV) oxide and 2,16g of water.
If the molecular mass of the hydrocarbon is 84, draw and name its molecular structure.
Since a hydrocarbon is a compound containing Carbon and Hydrogen only. Then:
Mass of carbon in CO2 = Mass of C in CO2 x mass of CO2 =>
Molar mass of CO2
12 x 5.28 = 1.44g√
44
Mass of Hydrogen in H2O = Mass of C in H2O x mass of H2O =>
Molar mass of H2O
2 x 2.16 = 0.24g√
18
| Element | Carbon | Hydrogen |
| Symbol | C | H |
| Moles present = mass Molar mass | 1.44g 12 | 0.24g√ 1 |
| Divide by the smallest value | 0.12 0.12 | 0.24 0.12 |
| Mole ratios | 1 | 2√ |
Empirical formula is CH2√
The molecular formular is thus determined :
n = Relative formular mass = 84 = 6√
Relative empirical formula 14
The molecular formula is (CH2 ) x 6 = C6H12. √
molecular name Hexene√/Hex-1-ene (or any position isomer of Hexene)
Molecular structure
H H H H H H
H C C C C C C H√
H H H H
5. Compound A contain 5.2% by mass of Nitrogen .The other elements present are Carbon, hydrogen and Oxygen. On combustion of 0.085g of A in excess Oxygen,0.224g of carbon(IV)oxide and 0.0372g of water was formed. Determine the empirical formula of A (N=14.0, O=16.0 , C=12.0 , H=1.0)
Mass of N in A = 5.2% x 0.085 = 0.00442 g
Mass of C in A = 12 x 0.224 = 0.0611g
44
Mass of H in A = 2 x 0.0372 = 0.0041g
18
Mass of O in A = 0.085g – 0.004442g = 0.0806g (Mass of C,H,O)
=> 0.0611g + 0.0041g = 0.0652g (Mass of C,H)
0.0806g (Mass of C,H,O)- 0.0652g (Mass of C,H) = 0.0154 g
| Element | Nitrogen | Carbon | Hydrogen | Oxygen |
| Symbol | N | C | H | O |
| Moles present = mass Molar mass | 0.00442 g 14 | 0.0611g 12 | 0.0041g 1 | 0.0154 g 16 |
| Divide by the smallest value | 0.00032 0.00032 | 0.00509 0.00032 | 0.0041g 0.00032 | 0.00096 0.00032 |
| Mole ratios | 1 | 16 | 13 | 3 |
Empirical formula = C16H13NO3
(d)Molar gas volume
The volume occupied by one mole of all gases at the same temperature and pressure is a constant.It is:
(i) 24dm3/24litres/24000cm3 at room temperature(25oC/298K)and pressure(r.t.p).
i.e. 1mole of all gases =24dm3/24litres/24000cm3 atr.t.p
Examples
1mole of O2 = 32g =6.0 x1023 particles= 24dm3/24litres/24000cm3 at r.t.p
1mole of H2 = 2g =6.0 x1023 particles =24dm3/24litres/24000cm3 at r.t.p
1mole of CO2 = 44g = 6.0 x1023 particles =24dm3/24litres/24000cm3 at r.t.p
1mole of NH3 = 17g =6.0 x1023 particles = 24dm3/24litres/24000cm3 at r.t.p
1mole of CH4 = 16g =6.0 x1023 particles =24dm3/24litres/24000cm3 at r.t.p
(ii)22.4dm3/22.4litres/22400cm3 at standard temperature(0oC/273K) and pressure(s.t.p)
i.e. 1mole of all gases =22.4dm3/22.4litres/22400cm3 ats.t.p
Examples
1mole of O2 = 32g =6.0 x1023 particles= 22.4dm3/22.4litres/22400cm3 at s.t.p
1mole of H2 = 2g =6.0 x1023 particles = 22.4dm3/22.4litres/22400cm3 at s.t.p
1mole of CO2 = 44g = 6.0 x1023 particles = 22.4dm3/22.4litres/22400cm3 at s.t.p
1mole of NH3 = 17g =6.0 x1023 particles= 22.4dm3/22.4litres/22400cm3 at s.t.p
1mole of CH4 = 16g =6.0 x1023 particles = 22.4dm3/22.4litres/22400cm3 at s.t.p
The volume occupied by one mole of a gas at r.t.p or s.t.p is commonly called the molar gas volume. Whether the molar gas volume is at r.t.p or s.t.p must always be specified.
From the above therefore a less or more volume can be determined as in the examples below.
Practice examples
1. Calculate the number of particles present in:
(Avogadros constant =6.0 x1023mole-1 )
(i) 2.24dm3 of Oxygen.
22.4dm3 -> 6.0 x1023
2.24dm3 -> 2.24 x 6.0 x1023
22.4
=6.0 x1022 molecules = 2 x 6.0 x1022. = 1.2 x1023 atoms
(ii) 2.24dm3 of Carbon(IV)oxide.
22.4dm3 -> 6.0 x1023
2.24dm3 -> 2.24 x 6.0 x1023
22.4
=6.0 x1022 molecules = (CO2) = 3 x 6.0 x1022. = 1.8 x1023 atoms
2. 0.135 g of a gaseous hydrocarbon X on complete combustion produces 0.41g of carbon(IV)oxide and 0.209g of water.0.29g of X occupy 120cm3 at room temperature and 1 atmosphere pressure .Name X and draw its molecular structure.(C=12.0,O= 16.O,H=1.0,1 mole of gas occupies 24dm3 at r.t.p)
Molar mass CO2= 44 gmole-1√ Molar mass H2O = 18 gmole-1√
Molar mass X = 0.29 x (24 x 1000)cm3 = 58 gmole-1√
120cm3
Since a hydrocarbon is a compound containing Carbon and Hydrogen only. Then:
Mass of carbon in CO2 = Mass of C in CO2 x mass of CO2 =>
Molar mass of CO2
12 x 0.41 = 0.1118g√
44
Mass of Hydrogen in H2O = Mass of C in H2O x mass of H2O =>
Molar mass of H2O
2 x 0.209 = 0.0232g√
18
| Element | Carbon | Hydrogen |
| Symbol | C | H |
| Moles present = % composition Molar mass | 0.g118 12 | 0.0232g√ 1 |
| Divide by the smallest value | 0.0093 0.0093 | 0.0232 0.0093√ |
| Mole ratios | 1 x2 | 2.5×2 |
| 2 | 5√ |
Empirical formula is C2H5√
The molecular formular is thus determined :
n = Relative formular mass = 58 = 2√
Relative empirical formula 29
The molecular formula is (C2H5 ) x 2 = C4H10.√
Molecule name Butane
Molecula structure
H H H H
H C C C C H√
H H H H
(e)Gravimetric analysis
Gravimetric analysis is the relationship between reacting masses and the volumes and /or masses of products. All reactants are in mole ratios to their products in accordance to their stoichiometric equation. Using the mole ration of reactants and products any volume and/or mass can be determined as in the examples:
1. Calculate the volume of carbon(IV)oxide at r.t.p produced when 5.0 g of calcium carbonate is strongly heated.(Ca=40.0, C= 12.0,O = 16.0,1 mole of gas =22.4 at r.t.p)
Chemical equation
CaCO3(s) -> CaO(s) + CO2(g)
Mole ratios 1: 1: 1
Molar Mass CaCO3 =100g
Method 1
100g CaCO3(s) -> 24dm3 CO2(g) at r.t.p
5.0 g CaCO3(s) -> 5.0 g x 24dm3 = 1.2dm3/1200cm3
100g
Method 2
Moles of 5.0 g CaCO3(s) = 5.0 g = 0.05 moles
100 g
Mole ratio 1:1
Moles of CO2(g) = 0.05moles
Volume of CO2(g) = 0.05 x 24000cm3 =1200cm3 /1.2dm3
2. 1.0g of an alloy of aluminium and copper were reacted with excess hydrochloric acid. If 840cm3 of hydrogen at s.t.p was produced, calculate the % of copper in the alloy.(Al =27.0,one mole of a gas at s.t.p =22.4dm3 )
Chemical equation
Copper does not react with hydrochloric acid
2Al(s) + 6HCl(aq) -> 2AlCl3(aq) + 3H2(g)
Method 1
3H2(g) = 3 moles x (22.4 x 1000)cm3 => 2 x 27 g Al
840cm3 => 840cm3 x 2 x 27 = 0.675g of Aluminium
3 x 22.4 x 1000
Total mass of alloy – mass of aluminium = mass of copper
=> 1.0g – 0.675g =0.325g of copper
% copper = mass of copper x100% = 32.5%
Mass of alloy
Method 2
Mole ratio 2Al: 3H2 = 2:3
Moles of Hydrogen gas = volume of gas => 840cm3 = 0.0375moles
Molar gas volume 22400cm3
Moles of Al = 2/3 moles of H2 => 2/3x 0.0375moles = 0.025moles
Mass of Al = moles x molar mass =>0.025moles x 27 = 0.675g
Total mass of alloy – mass of aluminium = mass of copper
=> 1.0g – 0.675g = 0.325 g of copper
% copper = mass of copper x100% = 32.5%
Mass of alloy
(f)Gay Lussac’s law
Gay Lussacs law states that “when gases combine/react they do so in simple volume ratios to each other and to their gaseous products at constant/same temperature and pressure”
Gay Lussacs law thus only apply to gases
Given the volume of one gas reactant, the other gaseous reactants can be deduced thus:
