- Evaluate without using a calculator . (3 marks)

- The sum of the ages of three brothers; Mike, Charles and Abdul is 65 years. Mike is twice as old as Abdul and one and half times as old as Charles. Determine their ages. (3 marks)
- A supermarket has 18 apples, 30 oranges and 54 apples. The fruits are to be arranged in rows such that every row contains same number of fruits of one type only. Determine the least number of rows required for this arrangement to happen. (3 marks)
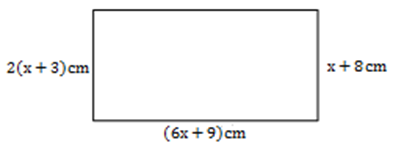
- Find the area of the rectangle below. (3 marks)
5. Without using a Calculator or Mathematical Table evaluate the value of p:

(3 marks)
Calculate the value of x given that . (3 marks)

- Solve for k in the equation . (2 marks)
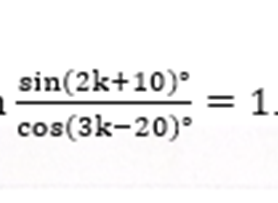
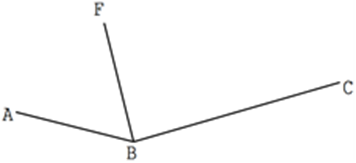
- In the figure below ABF is a uniform cross section of a solid. AB, BC and BF are some of the visible edges of the solid. Complete the sketch showing the hidden edges with broken lines. (3 marks)
- Mr. Charles who deals in electronics sells a radio to a customer at Kshs. 1,440 after giving him a discount of 10% but finds that he still makes a 20% profit. Find the profit Mr. Charles would make if he does not give a discount. (3marks)
The figure below shows a set of two right angled triangles ABD and BCD conjoined by side BD. Sides AB, BC and AD are 6cm, 5cm and 10cm in lengths respectively.
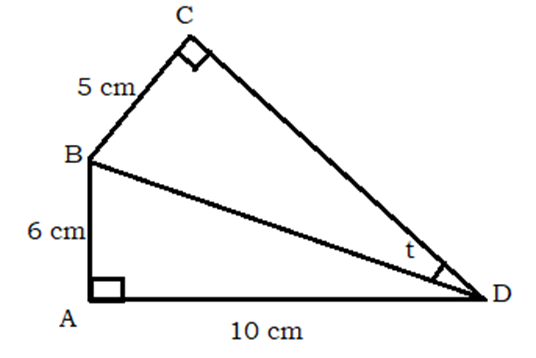
Calculate the size of angle CDB=t. (4 marks)
Two towns A and B are 810km apart. A car left A at 8:00am moving towards B at an average speed of xkm/h. A bus left town B at 9:30am moving towards A at an average speed of 84km/h. Determine the average speed of the car, xkm/h, if the two vehicles met at 11.00am. (4 marks)
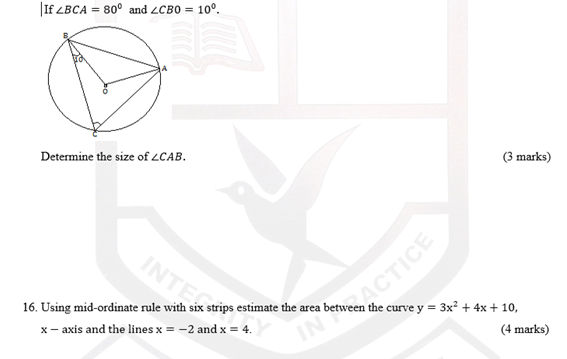
- In the figure given below, O is the centre of circle. If and
- Construct AIBICIDI the image of quadrilateral ABCD below. Given that it undergoes under transformation enlargement with scale factor -2 and centre O. (3 marks)

- The equation of line l1 is 2x+3y+ 6= 0.
- Find the gradient of line l1 (1 mark)
- The line l2 is perpendicular to l1 and passes through the point P with coordinates (7, 2), find the equation of l2 , giving the answer in the form y= mx+ c where m and c are constants. (3 marks)
- The line l1 and l2 intersect at point Q. Find the coordinates of Q. (3 marks)
- The line l3 is parallel to l1 and passes through point P. Find the equation of l3 giving the answer in the form ax+ by = c , where a , b and c are constants. (2 marks)
- Determine the x and y-intercepts of the line l3. (1 mark)
- The Form Two Parents of Ushindi High School decided to buy laboratory equipment worth Kshs.900,000 by each student contributing equal amount of money. Before they made the contribution 50 students got transferred to other institutions and this made the remaining students to pay Kshs.600 more.
- Taking to represent the original number of students, write down an expression for:
- The original contribution per student. (1 mark)
- The new contribution per student. (1 mark)
- Find the original number of students who were to contribute. (4 marks)
- Calculate the percentage change in the students’ contributions. (2 marks)
- If the ratio of boys to girls that remained in Form 2 was 13:12 calculate the amount contributed by the boys alone. (2 marks)
- Two circles of radii 3.5 and 4.2 cm with centres O1 and O2 respectively intersect at points A and B as shown in the figure below. The distance between the two centres is 6 cm and the distance from O1 to the common chord AB along O1O2 is x cm.
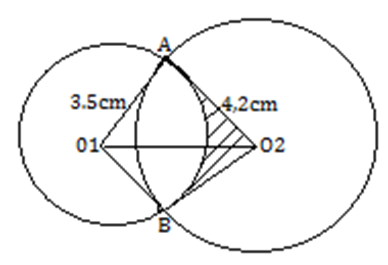
Calculate:
- The distance x cm to 3 decimal places. (3 marks)
- The size of ∠AO1B and ∠AO2 B (to the nearest degree). (3 marks)
- The area of quadrilateral O1AO2B, correct to 2 decimal place (2 marks)
- The shaded area correct to two significant figures. (Take. ). (2 marks)
- Three towns A, B and C are such that B is 120km on a bearing of 0600 from A. C lies directly East of A on a bearing 1650 from B. Using a scale of 1cm to represent 20km, a pair of compass and a ruler only, determine:
- the relative positions of A, B and C. (3 marks)
- drop a perpendicular from B to meet AC at M hence measure BM. (2 marks)
- construct a circle passing through the vertices A, B and C then calculate the area covered in the circle. (2 marks)
- Determine the amount of money used in ploughing the land inside the circle but outside triangle ABC at a rate of Kshs. 5000 per hectare. (3 marks)
- A solid is partly a cone and partly an hemisphere of radius 7cm. The slanting length of the cone is 25cm. Determine;
- the height of the solid. (2 marks)the volume of the solid (3 marks)
- the surface area of the solid. (3 marks)
- the mass of the solid if its density is 12.5g/cm3. (2 marks)
