MATHEMATICS Form 3 OCTOBER 2024
TIME: 2 ½ HOURS
END OF TERM THREE EXAMINATION
Kenya Certificate of Secondary Education 2024
SECTION I (50 Marks) Form Three Mathematics
Answer all the questions in this section in the spaces provided.
- Without using tables or calculator evaluate (3 marks)
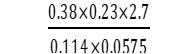
2. All prime numbers less than ten are arranged in descending order to form a number. Write the number formed (1 mark)
3. State the total value of the second digit in the number formed in (a) above (1 mark)
Use reciprocals, square and square roots tables to evaluate, to 4 significant figures, (4 marks) (3 marks)
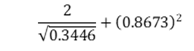
4.
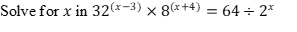
(3marks)
5.
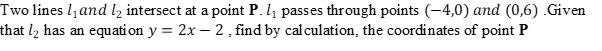
6. The length of a rectangle is (x+3) cm. If the width of the rectangle is two thirds its length and the perimeter is 40 cm, find its width. (3 marks)
7. A Kenyan bank buys and sells currencies at the exchange rates below

An American tourist arrived in Kenya with 24,000 Euros He converted all the Euros to Kenya shillings at the bank .He spent a total of Sh. 200,000 while in Kenya and converted the rest to into US dollars at the bank. Find the amount in dollars that he received to the nearest whole number.
8. In the figure below AB is parallel to DE ,DE bisects angle BDG , (3 marks)
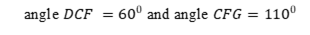
Find giving reasons for your answers
- <CDF (2 marks)
- <ABD (1 mark)
9. Find the inequalities that satisfy the region R shown in the figure below. (3 marks)

10. (i) Solve for x given that
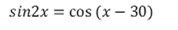
(ii) Hence find the value of
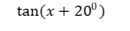
11. In the figure below ABCD is a cyclic quadrilateral and BD is a diagonal EADF is a straight line,

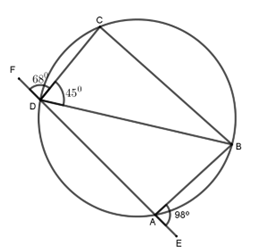
Calculate the size of
- <ADB (2 marks)
- <ABD (2mks)
12. A cube of metal of side 6.7 cm was melted and the molten material used to make a sphere. Find to 4 significant figures the radius of the sphere.
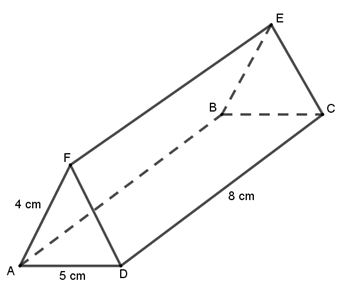
13. The figure below is a triangular prism of uniform cross-section in which AF=BE=4cm AD=5cm and DC=8cm.Draw a clearly labeled net of the prism. (3 marks)
14. Simplify the expression
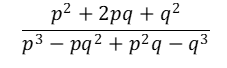
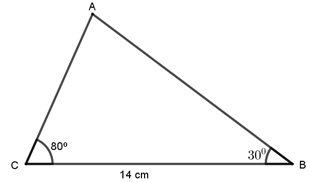
15. In the triangle ABC below, BC = 14 cm, ∠ABC=30° and ∠ACB=80°
16. The figure below is a velocity time graph of a car

Form 3 Mathematics SECTION II (50 marks)
Answer any five questions in this section only
- (a) Complete the table below for
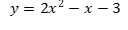

(b) Draw the graph
(b) Using a suitable straight line, solve
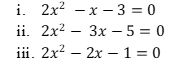
18. (a) The length of each side of an equilateral triangle ABC is 12 cm. Calculate the area of the triangle correct to 2 decimal places. (2 marks)
(b) The triangle ABC in (a) forms the base of a solid triangular pyramid VABC. The perpendicular height of the pyramid is 21 cm. Calculate the volume of the pyramid.(2 marks)
(c) The pyramid VABC in (b) above is recast into a cone of base radius 4.2 cm. Calculate, correct to 2 decimal places:
- The slant height of the cone. (2 marks)
- The surface area of the cone. (4 marks)
19. Four towns P,Q,R and S are such that Q is 350km on a bearing of from town P. Town R is 500km from town Q and on a bearing of from town Q .Town S is 600km due south of town Q
Using a scale of 1cm to represent 100km, draw a diagram to show the relative positions of town P,Q ,R and S (4 marks)
- Find the bearing and distance of
- P from S (2 marks)
- S from R (2 marks)
- Calculate the actual area bounded by PQ, QR, RS and PS to the nearest whole number. (2 marks)
20. The vertices of a triangle PQR are and Draw triangle PQR on the grid provided. (1 mark)

1. A school intended to buy a certain number of chairs for Ksh 16 200. The supplier
agreed to offer a discount of Ksh 60 per chair which enabled the school to get
3 more chairs. Taking x as the originally intended number of chairs,a)
Write an expression in terms of x for:
i. Original price per chair. (1 mark)
ii. Price per chair after discount. (1 mark)
b) Determine:i. The number of chairs the institution intended to buy. (4 marks)
ii. Price per chair after discount. (2 marks)
iii. The amount of money the institution would have saved per chair if it bought the
intended number of chairs at a discount of 15%. (2 marks)
22. In the figure below A and B are centres of the circle intersecting at point P and Q angle


Determine
a) The length of AB (3 marks)
b) Area of sector PBQ (2 marks)
c) Area of quadrilateral APBQ (3 marks)
d) Area of the shaded region (2 marks)
- Two alloys A and B, are each made up of copper, zinc and tin. In alloy A ,the ratio of copper to zinc is 3:2 and the ratio of zinc to tin is 3:5
a) Determine the ratio, copper: zinc: tin, in alloy A. (2 marks)
b) The mass of alloy A is 250 kg. Alloy B has the same mass as alloy A but the amount of copper is 30% less than that of alloy A .Calculate
i) The mass of tin in alloy A ; (2 marks)
ii) The total mass of zinc and tin in alloy B (3 marks)
iii) Given that the ratio of zinc to tin in alloy B is 3:8, determine the amount of tin in alloy B than in alloy A (3 marks)
24. The examination marks in a Geography test for 60 students were as follows:
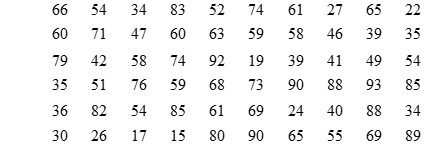
a) Complete the frequency distribution table below for the above examination. Use classes
of size 10 starting with the class (4 marks)

b) State the modal class. (1 mark)c)
Estimate:
i. The mean mark. (2 marks)
ii. The median mark. (3 marks)
